

Next: 根軌跡の利用
Up: 根軌跡法
Previous: 根軌跡(root locus)とは
根軌跡を描くに当たっては、表1.7に示す法則を用いると、その概形が容易に描ける。
表 1.7:
根軌跡の法則
| No. |
項目 |
法則 |
| 1 |
対称性 |
実軸に対して対称である |
| 2 |
起点 |
一巡伝達関数の極 |
| 3 |
終点 |
一巡伝達関数の零点叉は無限遠 |
| 4 |
軌跡の数 |
一巡伝達関数の極の数 |
| 5 |
無限遠に延びる |
(一巡伝達関数の極の数) |
| |
軌跡の数 |
ー (一巡伝達関数の零点の数) |
| 6 |
|
極、零点が総て実軸上にあるとき、 |
| |
実軸上の根軌跡 |
右側にある極と零点の個数の和が |
| |
|
奇数である所に根軌跡が存在する |
| 7 |
無限遠に延びる |
実軸と漸近線とのなす角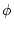 は は |
| |
軌跡の漸近線 |
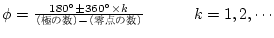 |
| 8 |
漸近線と |
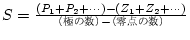 |
| |
実軸の交点 |
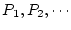 極 極
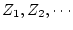 零点 零点 |
| |
|
(1)極、零点が実軸上にある場合 |
| |
|
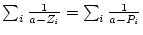 |
| 9 |
根軌跡と |
(2)極、零点が複素数の場合 |
| |
実軸との交点 |
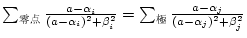 |
| |
|
ただし、
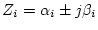 |
| |
|
,
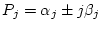 |
| 10 |
極から出る角 |
(出入角)=
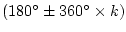 |
| |
叉は |
ー(他の極からの角) |
| |
零点に入る角 |
+(他の零点からの角) |
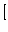 例
例
![$]KG=\frac{K(s+2)}{s(s+1)(s+3)}$](img456.png) の場合
の場合
1
20D実軸に対し対称となる。
2
20D起点
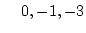
3
20D終点
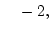 無限遠
無限遠
4
20D軌跡の数
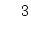
5
20D無限遠に延びる軌跡の数
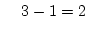
6
20D実軸上の根軌跡
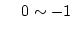 および
および 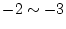 の間
の間
7
20D無限遠に延びる軌跡の漸近線
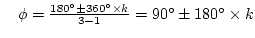
8
20D漸近線と実軸の交点
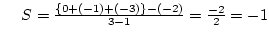
9
20D根軌跡と実軸の交点
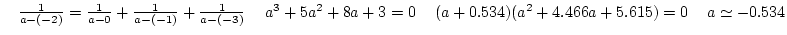
10
20D極から出る角、零点へ入る角
極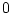 から出る角
から出る角
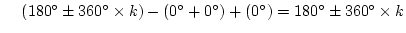
極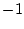 から出る角
から出る角
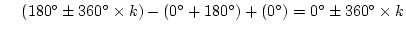
極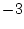 から出る角
から出る角
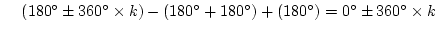
零点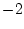 へ入る角
へ入る角
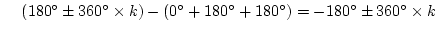
以上に基づき根軌跡を描いたのが図1.39である。
図:
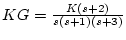 の場合の根軌跡
の場合の根軌跡
![\begin{figure}\begin{center}
\psbox[scale=0.50]{eps/1-7-3.eps} \end{center} \end{figure}](img474.png) |


Next: 根軌跡の利用
Up: 根軌跡法
Previous: 根軌跡(root locus)とは
Yasunari SHIDAMA
平成15年4月9日
![\begin{figure}\begin{center}
\psbox[scale=0.50]{eps/1-7-3.eps} \end{center} \end{figure}](img474.png)