

Next: 拡張変換
Up: 過度応答と周波数応答
Previous: 過度応答
いま入力信号が正弦波の場合
![\begin{displaymath}
U(Z)=Z\left[{\cal L}(e^{j \omega t})\right]=
\frac{1}{1-Z^{-1}e^{j \omega T}}
\end{displaymath}](img231.png) |
(3.40) |
とする。そのとき、出力は
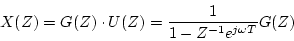 |
(3.41) |
となるから、これを逆変換すると
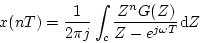 |
(3.42) |
となる。特異点は
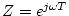 および
および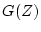 の極であるが、
定常状態では、後者の項は消えるので
の極であるが、
定常状態では、後者の項は消えるので
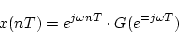 |
(3.43) |
となる。パルス列の包絡線は
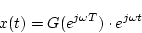 |
(3.44) |
となる。したがって入力正弦波と出力パルス列の包絡線に
対する周波数伝達関数は
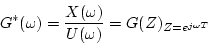 |
(3.45) |
となる。すなわち周波数応答のパルス伝達関数に
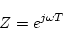 |
(3.46) |
を代入することにより、そのゲイン特性、位相特性が求められる。
但し、周波数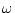 を
を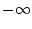 から
から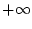 に変化させても、(3.46)
式の
に変化させても、(3.46)
式の は
は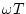 が
が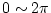 ごとに同一の値をとるので、
周波数応答は
ごとに同一の値をとるので、
周波数応答は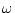 を
を
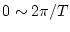 の範囲とればよい。
の範囲とればよい。
[例]
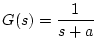 の周波数応答を求める。
の周波数応答を求める。
であるから、
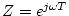 を代入すると
を代入すると
となる。したがってゲイン及び位相は
となる。
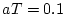 の場合に対し
の場合に対し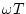 を横軸にとりボード線図を描いたのが
図3.15である。
を横軸にとりボード線図を描いたのが
図3.15である。
図 3.15:
![\begin{figure}\begin{center}
\psbox[scale=1.0]{eps/3-4-3.eps} \end{center} \end{figure}](img249.png) |
Yasunari SHIDAMA
平成15年6月9日
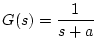 の周波数応答を求める。
の周波数応答を求める。
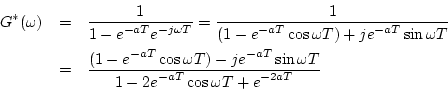
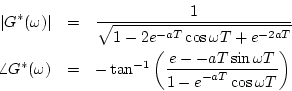
![]() の場合に対し
の場合に対し![]() を横軸にとりボード線図を描いたのが
図3.15である。
を横軸にとりボード線図を描いたのが
図3.15である。