

Next: 周波数応答
Up: 過度応答と周波数応答
Previous: 過度応答と周波数応答
(3.31)式より
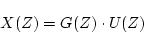 |
(3.35) |
の関係があるから、入力の 変換
変換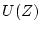 にパルス伝達関数を掛ければ
出力が得られ、その逆
にパルス伝達関数を掛ければ
出力が得られ、その逆 変換を求めれば過度応答が求められる。
すなわち
変換を求めれば過度応答が求められる。
すなわち
![\begin{displaymath}
x(nT)=Z^{-1}[G(Z) \cdot U(Z)]
\end{displaymath}](img219.png) |
(3.36) |
である。
インパルス入力の時
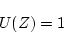 |
(3.37) |
ステップ入力の時
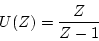 |
(3.38) |
ランプ入力の時
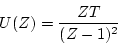 |
(3.39) |
である。
[例]
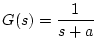 のステップ応答を求める。
のステップ応答を求める。
図 3.13:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-4-1.eps} \end{center} \end{figure}](img224.png) |
特異点は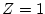 および
および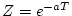 ゆえ
ゆえ
となる。
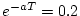 のときの応答が図3.7である。
のときの応答が図3.7である。
図3.14は極の位置と過度応答の形の関係を示している。
単位円に最も近い根が代表根であり、根が原点にあるときが最も減衰が速い。
図 3.14:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-4-2.eps} \end{center} \end{figure}](img230.png) |
Yasunari SHIDAMA
平成15年6月9日
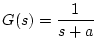 のステップ応答を求める。
のステップ応答を求める。
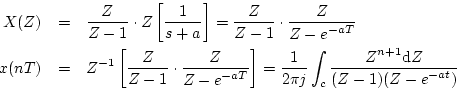
![]() のときの応答が図3.7である。
のときの応答が図3.7である。