

Next: 拡張したRouth-Hurwitzの安定判別法
Up: 安定判別
Previous: 安定判別
図3.18に示す閉回路のパルス伝達関数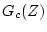 は
は
}
\end{displaymath}](img290.png) |
(3.54) |
であり、特性方程式は
=0
\end{displaymath}](img291.png) |
(3.55) |
である。特性根を
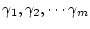 とすると(3.54)式は部分分数に展開でき
とすると(3.54)式は部分分数に展開でき
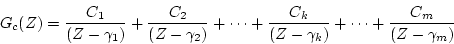 |
(3.56) |
となる。ただし重根のない場合であり、
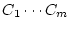 は定数である。
は定数である。
図 3.18:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-6-1.eps} \end{center} \end{figure}](img295.png) |
そこで、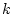 項について逆
項について逆 変換すると、
変換すると、
となるから
で表される。
いま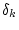 の実数部を
の実数部を
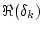 、虚数部を
、虚数部を
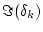 としたとき、
としたとき、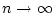 にした場合、上式は
にした場合、上式は
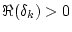 なら なら |
収束する |
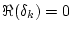 なら なら |
振動が持続する |
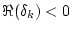 なら なら |
発散する |
そこで任意の極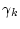 は
は
![\begin{displaymath}
\gamma_{k}=e^{-\delta_{k}T}=
\frac{\displaystyle 1}{\display...
...[\cos \{ -\Im(\delta_{k})T \} +
j\sin \{-\Im(\delta_{k})T \} ]
\end{displaymath}](img309.png) |
(3.59) |
と書けるから、
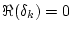 のとき、
のとき、
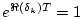 ゆえ、
ゆえ、
![\begin{displaymath}
\gamma_{k}=[\cos \{ -\Im(\delta_{k})T +
j\sin \{-\Im(\delta_{k})T \} ]
\end{displaymath}](img311.png) |
(3.60) |
となる。これが安定限界であって、単位円周上の点を意味している。
したがって、安定のためには
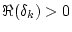 でなければならないから、
でなければならないから、 面上の極が全て
単位円内になければならない。このことから、
安定の条件は次のように云える。
面上の極が全て
単位円内になければならない。このことから、
安定の条件は次のように云える。
「パルス閉回路伝達関数の極が、全て 面の単位円内にあれば、
そのサンプル値系はサンプリング時刻に関する限り
安定であり、また一つでも極が単位円外に存在すれば、
不安定である。」
面の単位円内にあれば、
そのサンプル値系はサンプリング時刻に関する限り
安定であり、また一つでも極が単位円外に存在すれば、
不安定である。」


Next: 拡張したRouth-Hurwitzの安定判別法
Up: 安定判別
Previous: 安定判別
Yasunari SHIDAMA
平成15年6月9日
![]() 項について逆
項について逆![]() 変換すると、
変換すると、
![$\displaystyle Z^{-1}\left[\frac{\displaystyle C_{k}}
{\displaystyle Z-\gamma_{k}}\right]$](img296.png)
![]() の実数部を
の実数部を
![]() 、虚数部を
、虚数部を
![]() としたとき、
としたとき、![]() にした場合、上式は
にした場合、上式は
![]() 面の単位円内にあれば、
そのサンプル値系はサンプリング時刻に関する限り
安定であり、また一つでも極が単位円外に存在すれば、
不安定である。」
面の単位円内にあれば、
そのサンプル値系はサンプリング時刻に関する限り
安定であり、また一つでも極が単位円外に存在すれば、
不安定である。」