

Next: パルス回路網による補償方法
Up: サンプリング制御系の設計
Previous: サンプリングによる側帯波のうち重要成分のみを考慮する方法
いま閉回路のパルス伝達関数を
}{1+[HNG](Z)}
=K(Z)
\end{displaymath}](img393.png) |
(3.78) |
とすると、これを書き直すと
=\frac{K(Z)}{1-K(Z)}
\end{displaymath}](img394.png) |
(3.79) |
となる。そこで閉回路のパルス伝達関数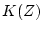 の形をあらかじめ規定すれば、
の形をあらかじめ規定すれば、$](img396.png) の伝達関数が逆に定まって来て、それより
の伝達関数が逆に定まって来て、それより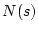 が求められる。
が求められる。
したがって次のような手順で設計を行う。
- #1.
- 要素性能に基づき
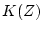 を規定する。
を規定する。
- #2.
-
=\frac{K(Z)}{1-K(Z)}$](img398.png) を求める。
を求める。
- #3.
- 上式に相当するラプラス伝達関数
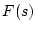 を求める。
を求める。
- #4.
-
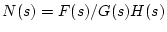 より補償要素
より補償要素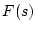 を求める。
を求める。
[例] 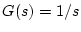 の補償対象で、ランプ入力に対して
定常偏差を零とする特性をもたせる。
の補償対象で、ランプ入力に対して
定常偏差を零とする特性をもたせる。
ランプ入力の場合
であるから定常偏差を零にするには
とする必要がある。この場合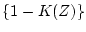 が
が
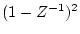 の項を含んでいればよいので
の項を含んでいればよいので
とすると
となり
となる。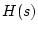 が零次ホールド回路の場合
が零次ホールド回路の場合
となり
となる。これを逆 変換して
変換して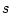 領域に戻すと
領域に戻すと
となり、
これが求める補償要素の伝達関数である。
Yasunari SHIDAMA
平成15年6月9日
![\begin{eqnarray*}
\left[\frac{N(s)G(s)}{S}\right]
& = & Z^{-1}\left[
\frac{T^{...
...3}} +
\frac{3}{2T}
\frac{1}{s^{2}}
=\frac{1+3Ts}{2T^{2}s^{3}}
\end{eqnarray*}](img413.png)