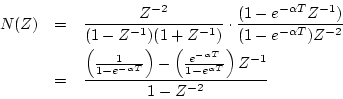

Next: この文書について...
Up: サンプリング制御系の設計
Previous: パルス回路網による補償方法
この方法は遅延要素を用いて、有限時間で整定を
させる方法である。
いま、図3.33に示すように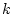 個の遅延要素と
増幅器を用いると、そのパルス伝達関数は
個の遅延要素と
増幅器を用いると、そのパルス伝達関数は
となる。次に図3.34の下側の回路に示すように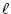 個の遅延要素と増幅器を用いてフィードバック回路を
構成すると、そのパルス伝達関数は
個の遅延要素と増幅器を用いてフィードバック回路を
構成すると、そのパルス伝達関数は
となり、図3.34全体のパルス伝達関数は
となる。この式は展開すると無限個の級数になり、
したがって任意の特性を得ることができることを示している。
図 3.33:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-8-10.eps} \end{center} \end{figure}](img430.png) |
図 3.34:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-8-11.eps} \end{center} \end{figure}](img431.png) |
例えば、図3.35の示す回路では
であるから、 変換すると
変換すると
となって、
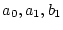 の組み合わせで
種々の形のものができる。そこで、
望ましい応答をあらかじめ定めておいて、
逆にこの補償回路を用いて特性改善をすることが
可能となる。
の組み合わせで
種々の形のものができる。そこで、
望ましい応答をあらかじめ定めておいて、
逆にこの補償回路を用いて特性改善をすることが
可能となる。
図 3.35:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-8-12.eps} \end{center} \end{figure}](img435.png) |
設計手順としては
- #1.
- 希望する閉回路パルス伝達関数
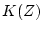 を決定する。
これはたとえば有限整定時間で応答するには表3.4の形を採用
する。ただし、制御対象の次数が
を決定する。
これはたとえば有限整定時間で応答するには表3.4の形を採用
する。ただし、制御対象の次数が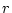 、むだ時間が
、むだ時間が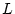 であった場合、
であった場合、
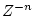 の
の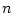 は整定迄の最小サンプリング数を表しているが、
この値を
は整定迄の最小サンプリング数を表しているが、
この値を
- #2.
- 一巡パルス伝達関数
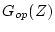 は
は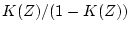 より求めるが、3.4表にも記載してある。
より求めるが、3.4表にも記載してある。
- #3.
- 制御装置のパルス伝達関数
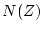 を次式より決定し、
((6))式より回路を構成する。
を次式より決定し、
((6))式より回路を構成する。
}
\end{displaymath}](img445.png) |
(3.80) |
[例]
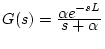 で
で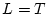 のとき、
のとき、
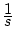 入力に対し有限時間で整定をさせる。
入力に対し有限時間で整定をさせる。
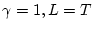 であるから、
であるから、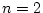 となり、
表3.4より
となり、
表3.4より
一方制御対象より
となるから制御装置の伝達関数は
となる。いま図3.36のような回路を構成すれば、
パルス伝達関数は
となるから
に設定すればよい。すなわち図3.37の
ような回路となり、この時の
操作量および制御量の変化は
図3.38のごとくなって、
2サンプリングで整定することがわかる。
図 3.36:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-8-13.eps} \end{center} \end{figure}](img472.png) |
図 3.37:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-8-14.eps} \end{center} \end{figure}](img473.png) |
図 3.38:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-8-15.eps} \end{center} \end{figure}](img474.png) |


Next: この文書について...
Up: サンプリング制御系の設計
Previous: パルス回路網による補償方法
Yasunari SHIDAMA
平成15年6月9日
![]() 個の遅延要素と
増幅器を用いると、そのパルス伝達関数は
個の遅延要素と
増幅器を用いると、そのパルス伝達関数は
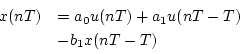
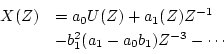
![]() で
で![]() のとき、
のとき、
![]() 入力に対し有限時間で整定をさせる。
入力に対し有限時間で整定をさせる。
![]() であるから、
であるから、![]() となり、
表3.4より
となり、
表3.4より