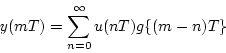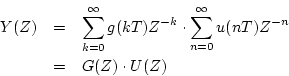

Next: パルス伝達関数
Up: サンプル値の表現と変換
Previous: 逆変換
 変換で用いられる主な定理を示すと次のごとくである。
変換で用いられる主な定理を示すと次のごとくである。
のときが、最大値(最小値)である。ゆえに
より、最大値(最小値)を生じる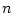 が求まる。
が求まる。
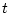 領域の微積分は、そのまま
領域の微積分は、そのまま 領域で行える。
領域で行える。
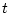 領域の極限は、そのまま
領域の極限は、そのまま 領域の極限に適用できる。
領域の極限に適用できる。
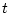 領域で
領域で
 にしたいときは、
にしたいときは、
 領域では
領域では
![$[F(Z)]_{Z=e^{sT}} \to [F(Z)]_{Z=e^{asT}}$](img177.png) となる。
となる。
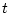 領域で
領域で
の関係があるとき、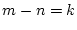 とすると
とすると 領域では
領域では
の関係がある。
Yasunari SHIDAMA
平成15年6月9日
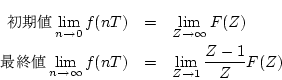
![\begin{eqnarray*}
{\cal L}\left[
\frac{\partial}
{\partial a}f^{*}(t,a)
\righ...
...*}(t,a){\mathrm d}a\right] & = &
\int_{0}^{a}F(Z,a){\mathrm d}a
\end{eqnarray*}](img174.png)
![]() 領域の微積分は、そのまま
領域の微積分は、そのまま![]() 領域で行える。
領域で行える。