

Next: 変換の諸定理
Up: サンプル値の表現と変換
Previous: 変換
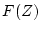 を逆変換したときには、各サンプル時点のときの値、
を逆変換したときには、各サンプル時点のときの値、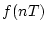 が求まる。
その定義式は
が求まる。
その定義式は
である。積分路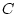 は
は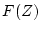 の全ての特異点を内部に含むような
閉曲線にとる。
の全ての特異点を内部に含むような
閉曲線にとる。
この積分を解くには、Cauchyの定理を適用し、留数を求める。
したがって、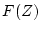 の根が重根を含まない場合の逆
の根が重根を含まない場合の逆 変換の手順は
変換の手順は
- #1.
-
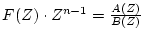 とする。
とする。
- #2.
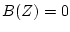 の根、
の根、
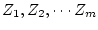 を求める。
を求める。
- #3.
-
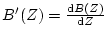 を求める。
を求める。
- #4.
-
![$f_{n}=Z^{-1}\left[F(Z)\right]=
\sum_{m=1}^{M}
\frac{A(Z_{m})}{B'(Z_{m})}$](img149.png)
が解である。
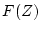 の根が
の根が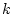 重根の場合は
重根の場合は
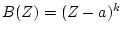 として
として
![\begin{displaymath}
f_{n}=Z^{-1}\left[F(Z)\right]=\frac{1}{(k-1)!}\frac{{\mathrm...
...}Z^{k-1}}
\left[ \frac{A(Z)}{(Z-a)^{k}}(Z-a)^{k} \right]_{Z=a}
\end{displaymath}](img152.png) |
(3.21) |
より求める。
[例1] 重根を含まない場合
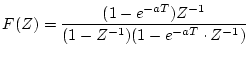 の逆変換を求める。
の逆変換を求める。
- #1.
-
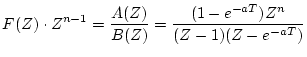
- #2.
-
![$\begin{array}[t]{l}
\displaystyle B(Z)=(Z-1)(Z-e^{-aT})=0 \\
\hspace*{2cm} \displaystyle Z_{1}=1,Z_{2}=e^{-aT}
\end{array}$](img155.png)
- #3.
-
![$\begin{array}[t]{ll}
\displaystyle B'(Z)
&=\displaystyle \frac{{\mathrm d}}{{...
...-Z(1+e^{-aT})+e^{-aT} \right\} \\
&=\displaystyle 2Z-(1+e^{-aT})
\end{array}$](img156.png)
- #4.
-
![$\begin{array}[t]{ll}
\displaystyle f_{n}
&=\displaystyle \frac{(1-e^{-aT})Z_...
...
{1-e^{-aT}}+
\frac{(1-e^{-aT})e^{-anT}}
{e^{-aT}-1}=1-e^{-anT}
\end{array}$](img157.png)
[例2] 重根の場合
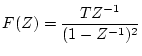 の逆
の逆 変換を求める。
変換を求める。
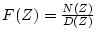 で与えられたとき、級数に展開し、
で与えられたとき、級数に展開し、
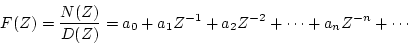 |
(3.22) |
となるから、
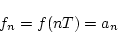 |
(3.23) |
より求める。
[例]
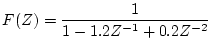 の逆
の逆 変換を求める。
変換を求める。
すなわち
となり、これを時間領域に戻すと
となる。これを図示したのが図3.7である。
これからもわかるように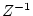 は1サンプリング遅延することを意味している。
は1サンプリング遅延することを意味している。
図 3.7:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-2-6.eps} \end{center} \end{figure}](img168.png) |


Next: 変換の諸定理
Up: サンプル値の表現と変換
Previous: 変換
Yasunari SHIDAMA
平成15年6月9日
![]() の根が重根を含まない場合の逆
の根が重根を含まない場合の逆![]() 変換の手順は
変換の手順は
![]() の根が
の根が![]() 重根の場合は
重根の場合は
![]() として
として
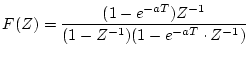 の逆変換を求める。
の逆変換を求める。
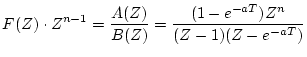
![$\begin{array}[t]{l}
\displaystyle B(Z)=(Z-1)(Z-e^{-aT})=0 \\
\hspace*{2cm} \displaystyle Z_{1}=1,Z_{2}=e^{-aT}
\end{array}$](img155.png)
![$\begin{array}[t]{ll}
\displaystyle B'(Z)
&=\displaystyle \frac{{\mathrm d}}{{...
...-Z(1+e^{-aT})+e^{-aT} \right\} \\
&=\displaystyle 2Z-(1+e^{-aT})
\end{array}$](img156.png)
![$\begin{array}[t]{ll}
\displaystyle f_{n}
&=\displaystyle \frac{(1-e^{-aT})Z_...
...
{1-e^{-aT}}+
\frac{(1-e^{-aT})e^{-anT}}
{e^{-aT}-1}=1-e^{-anT}
\end{array}$](img157.png)
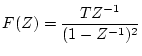 の逆
の逆![]() 変換を求める。
変換を求める。
![\begin{eqnarray*}
k=2\mbox{ゆえ} & & \\
f_{n}
& = & Z^{-1}\left[\frac{TZ}
{(Z...
...& \frac{{\mathrm d}}{{\mathrm d}Z}
\left[TZ^{n}\right]_{Z=1}=nT
\end{eqnarray*}](img159.png)
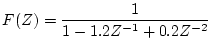 の逆
の逆![]() 変換を求める。
変換を求める。
![\begin{figure}\begin{center}
\psbox[scale=0.9]{eps/3-2-6a.eps} \end{center}\end{figure}](img164.png)
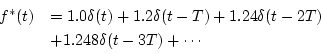
![]() は1サンプリング遅延することを意味している。
は1サンプリング遅延することを意味している。