

Next: 結合法則
Up: パルス伝達関数
Previous: パルス伝達関数
いま図3.8において、サンプラ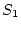 と
と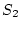 が同期して開閉する
ものとする。入力
が同期して開閉する
ものとする。入力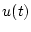 がサンプリングされてパルス列
がサンプリングされてパルス列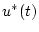 となり、こ
れが
となり、こ
れが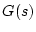 なる伝達関数をもつ伝達要素に加わる。伝達要素を通過すると各パル
スはインパルス応答をするので、伝達要素の出力は再び連続信号となる。すなわ
ち出力
なる伝達関数をもつ伝達要素に加わる。伝達要素を通過すると各パル
スはインパルス応答をするので、伝達要素の出力は再び連続信号となる。すなわ
ち出力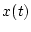 となる。これを再度サンプリングするとパルス列
となる。これを再度サンプリングするとパルス列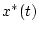 となる。
となる。
図 3.8:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-3-1.eps} \end{center} \end{figure}](img188.png) |
たとえば、図3.9に示すごとく入力として単位パルス列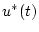 が伝達要素に加わったとする。その場合
が伝達要素に加わったとする。その場合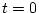 の時点から#1パルスの
インパルス応答が現れる。
の時点から#1パルスの
インパルス応答が現れる。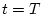 の時点ではその応答の一部が
まだ残っており、そこに更に#2のパルスのインパルス応答が加わる。
したがって出力パルス列
の時点ではその応答の一部が
まだ残っており、そこに更に#2のパルスのインパルス応答が加わる。
したがって出力パルス列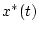 はこの両者の和となる。
はこの両者の和となる。
さらに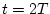 の時点では#3パルスのインパルス応答が加わることになる。
の時点では#3パルスのインパルス応答が加わることになる。
以上のごとく、出力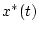 は各入力パルスのインパルス応答の和となる。
は各入力パルスのインパルス応答の和となる。
いま一般に入力パルス列を
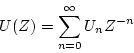 |
(3.24) |
とする。また出力パルス列を
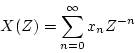 |
(3.25) |
とする。さらに、伝達要素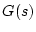 に単位パルスを加えたときの
出力パルスのパルス列を
に単位パルスを加えたときの
出力パルスのパルス列を
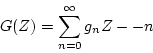 |
(3.26) |
とする。
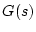 に
に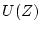 のパルス列を加えた時の出力は
のパルス列を加えた時の出力は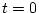 の時点で
の時点で
![\begin{displaymath}
x_{0}Z^{0}=[g_{0}Z^{0}] \cdot [u_{0}Z^{0}]
\end{displaymath}](img196.png) |
(3.27) |
となり、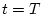 の時点で
の時点で
![\begin{displaymath}
x_{1}Z^{-1}=[g_{1}Z^{-1}][u_{0}Z^{0}]+[g_{0}Z^{0}][u_{1}Z^{-1}]
\end{displaymath}](img197.png) |
(3.28) |
となる。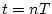 の時点では
の時点では
![\begin{displaymath}
x_{n}Z^{-n}=[g_{n}Z^{-n}][u_{0}Z^{0}]+ \cdots +[g_{0}Z^{0}][u_{n}Z^{-n}]
\end{displaymath}](img199.png) |
(3.29) |
となる。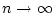 として以上を合計すると
として以上を合計すると
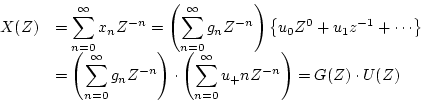 |
(3.30) |
となる。
したがって出力パルス列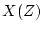 と入力パルス列
と入力パルス列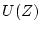 の比を求めると
の比を求めると
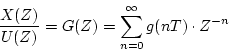 |
(3.31) |
となり、伝達関数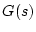 の
の 変換となる。これをパルス伝達関数という。
変換となる。これをパルス伝達関数という。
図 3.9:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-3-2.eps} \end{center} \end{figure}](img204.png) |


Next: 結合法則
Up: パルス伝達関数
Previous: パルス伝達関数
Yasunari SHIDAMA
平成15年6月9日
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/3-3-1.eps} \end{center} \end{figure}](img188.png)
![]() が伝達要素に加わったとする。その場合
が伝達要素に加わったとする。その場合![]() の時点から#1パルスの
インパルス応答が現れる。
の時点から#1パルスの
インパルス応答が現れる。![]() の時点ではその応答の一部が
まだ残っており、そこに更に#2のパルスのインパルス応答が加わる。
したがって出力パルス列
の時点ではその応答の一部が
まだ残っており、そこに更に#2のパルスのインパルス応答が加わる。
したがって出力パルス列![]() はこの両者の和となる。
はこの両者の和となる。
![]() の時点では#3パルスのインパルス応答が加わることになる。
の時点では#3パルスのインパルス応答が加わることになる。
![]() は各入力パルスのインパルス応答の和となる。
は各入力パルスのインパルス応答の和となる。
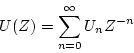
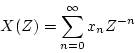
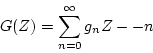
![]() に
に![]() のパルス列を加えた時の出力は
のパルス列を加えた時の出力は![]() の時点で
の時点で
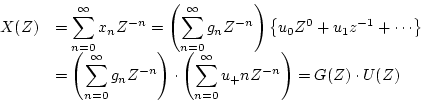
![]() と入力パルス列
と入力パルス列![]() の比を求めると
の比を求めると