


Next: 一般的手法
Up: 連続系の状態変数を離散値系で表示する方法
Previous: 連続系の状態変数を離散値系で表示する方法
前項では離散値信号のみで構成される場合の状態変数のとりかたを示したが、実
際の制御要素は連続系としての特性を持っている。したがって連続系としての状
態変数がある。それを離散値系の状態方程式で表示する方法について述べる。
一般にサンプリング系では図4.11に示すように零次ホールド回路を使用して連続信
号に変換して制御対象を駆動する。
図 4.11:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-3-1.eps} \end{center} \end{figure}](img132.png) |
いま、例として
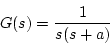 |
(4.53) |
の場合を考える。そして図4.12に示すように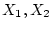 を状態変数に
とる。
を状態変数に
とる。
図 4.12:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-3-2.eps} \end{center} \end{figure}](img135.png) |
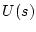 なる入力をサンプリングし、零次ホールドをすると、図4.13に
示すような各サンプリングにおける階段状の形
なる入力をサンプリングし、零次ホールドをすると、図4.13に
示すような各サンプリングにおける階段状の形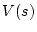 となる。
となる。
図 4.13:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-3-3.eps} \end{center} \end{figure}](img138.png) |
そこで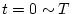 の間を考えると、制御対象への入力は
の間を考えると、制御対象への入力は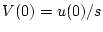 とな
る。
とな
る。
また、各状態変数の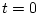 の時の初期条件を
の時の初期条件を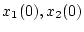 とすると、
図4.12より
とすると、
図4.12より
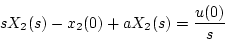 |
(4.54) |
となるから、
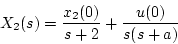 |
(4.55) |
と書ける。また
より
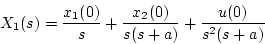 |
(4.56) |
と書ける。両式を逆変換すると
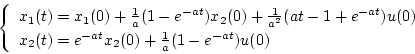 |
(4.57) |
となり、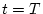 の時点では次式となる。
の時点では次式となる。
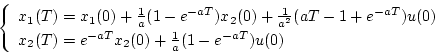 |
(4.58) |
この式は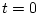 の値から
の値から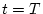 の値が決定されることを示している。そこで図
4.12に示すように、各状態変数の所に、人為的にサンプリングを入れ、
の値が決定されることを示している。そこで図
4.12に示すように、各状態変数の所に、人為的にサンプリングを入れ、
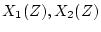 を考えると、任意のサンプリング時点
を考えると、任意のサンプリング時点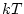 より、次のサンプリ
ング時点
より、次のサンプリ
ング時点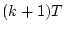 の値が求められるので(4.59)式から一般的に
の値が求められるので(4.59)式から一般的に
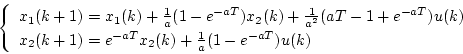 |
(4.59) |
で表現される。これが状態方程式となり
![\begin{displaymath}
\left.
\begin{array}{l}
\mbox{\boldmath$x$}(k+1) = \mbox{...
...\frac{1-e^{-aT}}{a}
\end{array} \right]
\end{array} \right\}
\end{displaymath}](img153.png) |
(4.60) |
と表示される。



Next: 一般的手法
Up: 連続系の状態変数を離散値系で表示する方法
Previous: 連続系の状態変数を離散値系で表示する方法
Yasunari SHIDAMA
平成15年6月30日
![]() なる入力をサンプリングし、零次ホールドをすると、図4.13に
示すような各サンプリングにおける階段状の形
なる入力をサンプリングし、零次ホールドをすると、図4.13に
示すような各サンプリングにおける階段状の形![]() となる。
となる。
![]() の間を考えると、制御対象への入力は
の間を考えると、制御対象への入力は![]() とな
る。
とな
る。
![]() の時の初期条件を
の時の初期条件を![]() とすると、
図4.12より
とすると、
図4.12より
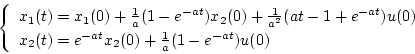
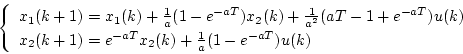
![\begin{displaymath}
\left.
\begin{array}{l}
\mbox{\boldmath$x$}(k+1) = \mbox{...
...\frac{1-e^{-aT}}{a}
\end{array} \right]
\end{array} \right\}
\end{displaymath}](img153.png)