


Next: 定常線形系の性質
Up: 連続系の状態変数を離散値系で表示する方法
Previous: 概要
一般的手法
次に連続系の状態方程式から、離散値系の状態方程式への一般的な変換法につい
て述べる。
いま、連続系の状態方程式を
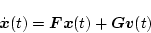 |
(4.61) |
とする。この解は、
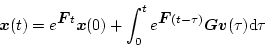 |
(4.62) |
である。前述の例と同様、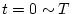 について考え、初期状態として
について考え、初期状態として
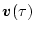 を
を
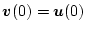 とし、
とし、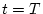 の最終状態は次のように
なる。
の最終状態は次のように
なる。
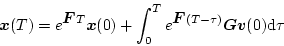 |
(4.63) |
いま
ただし
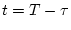
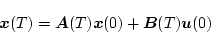 |
(4.66) |
となる。任意のサンプリング時点では
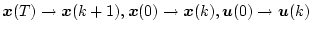 のようにおき
かえて
のようにおき
かえて
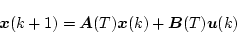 |
(4.67) |
とすれば離散値系の状態方程式となる。したがって、
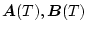 は
(4.65),(4.66)式より求めればよい。
は
(4.65),(4.66)式より求めればよい。
[例1]
![\begin{displaymath}
\left[
\begin{array}{c}
\dot{x}_1 \\
\dot{x}_2
\end{ar...
...t] +
\left[
\begin{array}{c}
0 \\
1
\end{array} \right]v
\end{displaymath}](img169.png) |
(4.68) |
より離散値系の状態方程式を求める。
上式より
したがって
となり、状態方程式は
![\begin{displaymath}
\left[
\begin{array}{c}
x_1(k+1) \\
x_2(k+1)
\end{arra...
...-aT}-1}{a^2} \\
\frac{1-e^{-aT}}{a}
\end{array} \right]u(k)
\end{displaymath}](img175.png) |
(4.71) |
となる。
[例2]デジタル回路を含む制御系
計算機制御系のようにデジタル回路を含む制御系では、制御対象は前項で述べた
ような連続系としての状態変数をとり、デジタル部分では直接法等による状態変
数を用いる必要がある。
図 4.14:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-3-4.eps} \end{center} \end{figure}](img176.png) |
いま次のような制御系を例として考える。デジタル回路のパルス伝達関数を次式
とする。
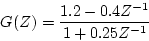 |
(4.72) |
図 4.15:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-3-5.eps} \end{center} \end{figure}](img178.png) |
これを直接法で表示すると
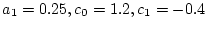 となるから中間変数を
となるから中間変数を
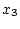 として
として
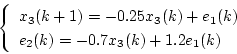 |
(4.73) |
が得られる。
制御対象は、Phase variableで表示すると
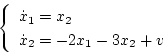 |
(4.74) |
となり
![\begin{displaymath}
\left[
\begin{array}{c}
\dot{x}_1 \\
\dot{x}_2
\end{ar...
...t] +
\left[
\begin{array}{c}
0 \\
1
\end{array} \right]v
\end{displaymath}](img183.png) |
(4.75) |
より
これを(4.23)式に代入して
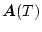 を求める場合、
(
を求める場合、
(![[*]](./icons/crossref.png) )式を用いて遷移行列
)式を用いて遷移行列
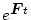 を求め
を求め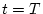 とすると
とすると
![\begin{displaymath}
\mbox{\boldmath$A$}(T)=
\left[
\begin{array}{cc}
2e^{-T}...
... \\
-2e^{-T}+2e^{-2T} & 2e^{-2T}-e^{-T}
\end{array} \right]
\end{displaymath}](img187.png) |
(4.76) |
また遷移行列を(4.66)式に代入すると
![\begin{displaymath}
\mbox{\boldmath$B$}(T) =
\left[
\begin{array}{c}
-e^{-T}...
...-2T}}{2}+\frac{1}{2} \\
-e^{-2T}+e^{-T}
\end{array} \right]
\end{displaymath}](img188.png) |
(4.77) |
となり、離散値系の状態方程式は
![\begin{displaymath}
\left[
\begin{array}{c}
x_1(k+1) \\
x_2(k+1)
\end{arra...
...2}+\frac{1}{2} \\
-e^{-2T}+e^{-T}
\end{array} \right]e_2(k)
\end{displaymath}](img189.png) |
(4.78) |
で表される。これを今簡単のため
![\begin{displaymath}
\left[
\begin{array}{c}
x_1(k+1) \\
x_2(k+1)
\end{arra...
...ft[
\begin{array}{c}
b_1 \\
b_2
\end{array} \right]e_2(k)
\end{displaymath}](img190.png) |
(4.79) |
で表す。
一方図より
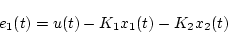 |
(4.80) |
から、各サンプリング時点では次式となる。
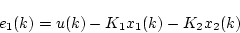 |
(4.81) |
(4.80)式の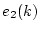 に(4.74)式および
(4.82)式を代入し、
に(4.74)式および
(4.82)式を代入し、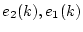 を消去すると次式が得られる。
を消去すると次式が得られる。
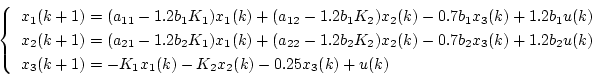 |
(4.82) |
これより状態方程式は
![\begin{displaymath}
\begin{array}{l}
\left[
\begin{array}{c}
x_1(k+1) \\
x_...
...2 \\
1
\end{array} \right]u(k)\\
y(k) = x_1(k)
\end{array}\end{displaymath}](img196.png) |
(4.83) |
で表される。



Next: 定常線形系の性質
Up: 連続系の状態変数を離散値系で表示する方法
Previous: 概要
Yasunari SHIDAMA
平成15年6月30日
![\begin{displaymath}
\left[
\begin{array}{c}
\dot{x}_1 \\
\dot{x}_2
\end{ar...
...t] +
\left[
\begin{array}{c}
0 \\
1
\end{array} \right]v
\end{displaymath}](img169.png)
![\begin{displaymath}
\mbox{\boldmath$F$} =
\left[
\begin{array}{cr}
0 & 1 \\ ...
...G$} =
\left[
\begin{array}{c}
0 \\
1
\end{array} \right]
\end{displaymath}](img170.png)
![$\displaystyle e^{\mbox{\boldmath$F$}T} = {\cal L}^{-1}\{(s\mbox{\boldmath$I$}-\...
...[
\begin{array}{cc}
s & -1 \\
0 & s + a
\end{array}\right]^{-1}
\right\}_{t=T}$](img171.png)
![$\displaystyle {\cal L}^{-1}
\left[
\begin{array}{cc}
\frac{1}{s} & \frac{1}{s(s...
...t[
\begin{array}{cc}
1 & \frac{1-e^{-at}}{a} \\
0 & e^{-at}
\end{array}\right]$](img172.png)
![$\displaystyle \int_0^T
\left[
\begin{array}{cc}
1 & \frac{1-e^{-at}}{a} \\
0 &...
...\begin{array}{c}
\frac{1-e^{-at}}{a} \\
e^{-at}
\end{array}\right]{\mathrm d}t$](img173.png)
![$\displaystyle \left[
\begin{array}{c}
\frac{aT + e^{-aT} -1}{a^2} \\
\frac{1-e^{-aT}}{a}
\end{array}\right]$](img174.png)
![\begin{displaymath}
\left[
\begin{array}{c}
x_1(k+1) \\
x_2(k+1)
\end{arra...
...-aT}-1}{a^2} \\
\frac{1-e^{-aT}}{a}
\end{array} \right]u(k)
\end{displaymath}](img175.png)
![]() となるから中間変数を
となるから中間変数を
![]() として
として
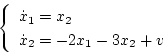
![\begin{displaymath}
\left[
\begin{array}{c}
\dot{x}_1 \\
\dot{x}_2
\end{ar...
...t] +
\left[
\begin{array}{c}
0 \\
1
\end{array} \right]v
\end{displaymath}](img183.png)
![\begin{displaymath}
\mbox{\boldmath$F$} =
\left[
\begin{array}{rr}
0 & 1 \\
...
...$G$}=
\left[
\begin{array}{c}
0 \\
1
\end{array} \right]
\end{displaymath}](img184.png)
![\begin{displaymath}
\mbox{\boldmath$A$}(T)=
\left[
\begin{array}{cc}
2e^{-T}...
... \\
-2e^{-T}+2e^{-2T} & 2e^{-2T}-e^{-T}
\end{array} \right]
\end{displaymath}](img187.png)
![\begin{displaymath}
\mbox{\boldmath$B$}(T) =
\left[
\begin{array}{c}
-e^{-T}...
...-2T}}{2}+\frac{1}{2} \\
-e^{-2T}+e^{-T}
\end{array} \right]
\end{displaymath}](img188.png)
![\begin{displaymath}
\left[
\begin{array}{c}
x_1(k+1) \\
x_2(k+1)
\end{arra...
...2}+\frac{1}{2} \\
-e^{-2T}+e^{-T}
\end{array} \right]e_2(k)
\end{displaymath}](img189.png)
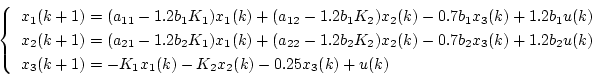
![\begin{displaymath}
\begin{array}{l}
\left[
\begin{array}{c}
x_1(k+1) \\
x_...
...2 \\
1
\end{array} \right]u(k)\\
y(k) = x_1(k)
\end{array}\end{displaymath}](img196.png)