


Next: 任意入力に対する過渡応答
Up: 定常線形系の性質
Previous: パルス伝達関数および固有値
自由系の場合、状態方程式は
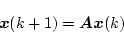 |
(4.94) |
であるので、
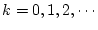 の各々の値に対して
の各々の値に対して
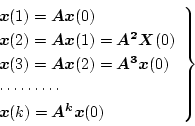 |
(4.95) |
となるから
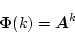 |
(4.96) |
とおき、これを遷移マトリクスと呼ぶ。これを代入すると
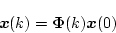 |
(4.97) |
となる。上式より、初期値
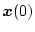 が与えられると、以後の状態ベクトルの
応答は遷移マトリクスを用いて得ることがある。
が与えられると、以後の状態ベクトルの
応答は遷移マトリクスを用いて得ることがある。
ここで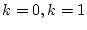 のとき
のとき
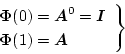 |
(4.98) |
である。
Yasunari SHIDAMA
平成15年6月30日
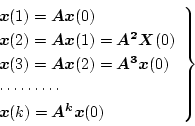
![]() のとき
のとき