


Next: 可制御性
Up: 定常線形系の性質
Previous: 遷移マトリクス(Transition Matrix)
状態方程式は
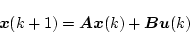 |
(4.99) |
であるから、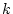 の各値に対して
の各値に対して
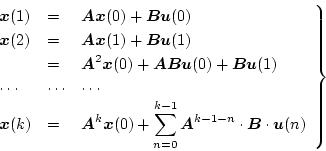 |
(4.100) |
となる。これを遷移マトリクスで表示すると
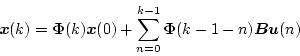 |
(4.101) |
となる。この式に各入力信号と初期値を与えれば過渡応答が計算される。
この式と(4.90)式と比較すると右辺の第1項の
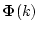 の
の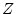 変換を
変換を
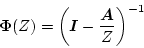 |
(4.102) |
とすると両辺の対応が得られ、第2項の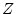 変換にConvolution(たたみ込み)定理を
適用すると
変換にConvolution(たたみ込み)定理を
適用すると
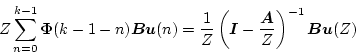 |
(4.103) |
となるので両式の対応が得られる。
したがって遷移マトリクスは(4.103)式の逆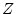 変換からも得ることが
できる。
変換からも得ることが
できる。
[例]次のシステム
![\begin{displaymath}
\left.
\begin{array}{l}
\left[
\begin{array}{c}
x_1(k+1...
... x_1(k) \\
x_2(k)
\end{array} \right]
\end{array} \right\}
\end{displaymath}](img227.png) |
(4.104) |
の過渡応答を求める。
(4.103)式より遷移マトリクスを求める。
したがって
![\begin{displaymath}
\left[
\begin{array}{c}
x_1(k) \\
x_2(k)
\end{array} \...
...]
\left[
\begin{array}{c}
0 \\
1
\end{array} \right]u(n)
\end{displaymath}](img233.png) |
(4.107) |
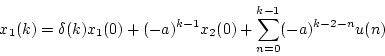 |
(4.108) |
ただし、この場合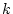 が0の時点以降に現象が生じるので、
が0の時点以降に現象が生じるので、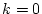 のとき
のとき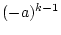 は0として扱う。すなわち
は0として扱う。すなわち
となり、(4.97),(4.99)式の関係と等しくなる。
(4.109)式の第3項は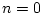 の時の入力
の時の入力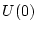 は
は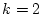 の時に始めて現
れてくることを意味している。
の時に始めて現
れてくることを意味している。



Next: 可制御性
Up: 定常線形系の性質
Previous: 遷移マトリクス(Transition Matrix)
Yasunari SHIDAMA
平成15年6月30日
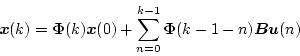
![]() の
の![]() 変換を
変換を
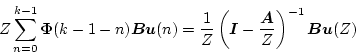
![]() 変換からも得ることが
できる。
変換からも得ることが
できる。
![\begin{displaymath}
\left.
\begin{array}{l}
\left[
\begin{array}{c}
x_1(k+1...
... x_1(k) \\
x_2(k)
\end{array} \right]
\end{array} \right\}
\end{displaymath}](img227.png)
![$\displaystyle \left(\mbox{\boldmath$I$}-\frac{\mbox{\boldmath$A$}}{Z}\right)^{-...
...eft[
\begin{array}{cc}
\frac{Z+a}{Z} & \frac{1}{Z} \\
0 & 1
\end{array}\right]$](img229.png)
![$\displaystyle \left[
\begin{array}{cc}
1 & \frac{1}{Z+a} \\
0 & \frac{Z}{Z+a}
\end{array}\right]$](img230.png)
![$\displaystyle Z^{-1}
\left[
\begin{array}{cc}
1 & \frac{1}{Z+a} \\
0 & \frac{Z...
...eft[
\begin{array}{cc}
\delta(k) & (-a)^{k-1} \\
0 & (-a)^k
\end{array}\right]$](img232.png)
![\begin{displaymath}
\left[
\begin{array}{c}
x_1(k) \\
x_2(k)
\end{array} \...
...]
\left[
\begin{array}{c}
0 \\
1
\end{array} \right]u(n)
\end{displaymath}](img233.png)
![\begin{displaymath}
\mbox{\boldmath$\Phi$}(0) =
\left[
\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array} \right]
\end{displaymath}](img237.png)
![\begin{displaymath}
\mbox{\boldmath$\Phi$}(k) =
\left[
\begin{array}{cc}
0 &...
...k
\end{array} \right]
\ \ \ \mbox{ただし $ k= 1,2,\cdots $}
\end{displaymath}](img238.png)