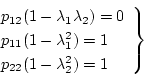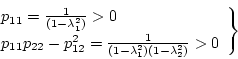Next: 離散値系の各種制御法
Up: 安定判別
Previous: リアプノフの安定判別法
システム方程式
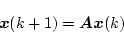 |
(4.131) |
リアプノフ関数
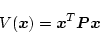 |
(4.132) |
とした場合
となる。
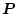 が正定で
が正定で
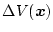 が負であれば漸近安定である。
が負であれば漸近安定である。
いま
![\begin{displaymath}[\mbox{\boldmath$A$}^T\mbox{\boldmath$PA$}-\mbox{\boldmath$P$}]= -\mbox{\boldmath$Q$}
\end{displaymath}](img316.png) |
(4.134) |
とし、
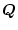 を正定にとる。その時(4.135)式より求めた
を正定にとる。その時(4.135)式より求めた
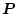 が正定すなわち
シルベスタの条件を満足すればこの系は漸近安定であるといえる。
が正定すなわち
シルベスタの条件を満足すればこの系は漸近安定であるといえる。
[例]図4.18の製御系の安定の判別をする。
図 4.18:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-5-3.eps} \end{center} \end{figure}](img318.png) |
伝達関数を部分分数に分解すると
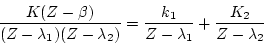 |
(4.135) |
となり、これを状態方程式で表示すると
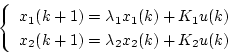 |
(4.136) |
となる。安定判別は自由系で考えればよいから
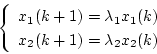 |
(4.137) |
とし、
![\begin{displaymath}
\mbox{\boldmath$x$}(k+1) =
\left[
\begin{array}{cc}
\lam...
... \\
0 & \lambda_2
\end{array} \right]\mbox{\boldmath$x$}(k)
\end{displaymath}](img322.png) |
(4.138) |
となる。いま
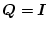 にとると
にとると
![\begin{displaymath}
\mbox{\boldmath$A$}^T\mbox{\boldmath$PA$}-\mbox{\boldmath$P...
...eft[
\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array} \right]
\end{displaymath}](img324.png) |
(4.139) |
となり
![\begin{displaymath}
\left[
\begin{array}{cc}
p_{11}(\lambda_1^2-1) & p_{12}(\...
...eft[
\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array} \right]
\end{displaymath}](img325.png) |
(4.140) |
となる。したがって
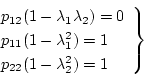 |
(4.141) |
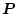 が正定であれば、安定であるから、シルベスタの条件
が正定であれば、安定であるから、シルベスタの条件
に上式を代入すると
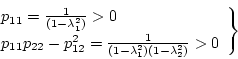 |
(4.142) |
より、安定の条件は
となる。これは離散値系状態方程式で表した場合、安定の為には特性方程式の根
が単位円内になければならないということを意味している。



Next: 離散値系の各種制御法
Up: 安定判別
Previous: リアプノフの安定判別法
Yasunari SHIDAMA
平成15年6月30日
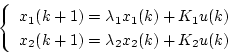
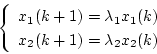
![\begin{displaymath}
\mbox{\boldmath$x$}(k+1) =
\left[
\begin{array}{cc}
\lam...
... \\
0 & \lambda_2
\end{array} \right]\mbox{\boldmath$x$}(k)
\end{displaymath}](img322.png)
![\begin{displaymath}
\mbox{\boldmath$A$}^T\mbox{\boldmath$PA$}-\mbox{\boldmath$P...
...eft[
\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array} \right]
\end{displaymath}](img324.png)
![\begin{displaymath}
\left[
\begin{array}{cc}
p_{11}(\lambda_1^2-1) & p_{12}(\...
...eft[
\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array} \right]
\end{displaymath}](img325.png)