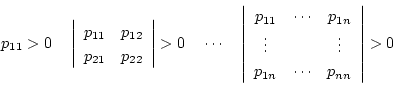Next: 線形系の安定判別法
Up: 安定判別
Previous: 安定の概念
連続系の場合と同様、平衡点を包囲し全状態変数より構成され、正定の値をもつ
リアプノフ関数
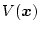 を考える。このリアプノフ関数が各サンプリング毎に
次第に縮小され、
を考える。このリアプノフ関数が各サンプリング毎に
次第に縮小され、
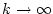 のとき
のとき
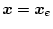 となり
となり
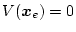 となって停止すれば安定であるといえる。
となって停止すれば安定であるといえる。
図 4.17:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-5-2.eps} \end{center} \end{figure}](img291.png) |
いま図4.17のような制御系を考える。この系の状態方程式は、自由系
として次のように書くことができる。
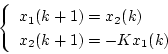 |
(4.123) |
いまリアプノフ関数を次のように定める。
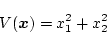 |
(4.124) |
このリアプノフ関数は正定であり、これが時間の経過と共に小さくなり原点に達
すれば漸近安定である。そこで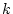 番目と
番目と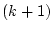 番目を比較し
番目を比較し
![\begin{displaymath}
\Delta V[\mbox{\boldmath$x$}(k)] = V[\mbox{\boldmath$x$}(k+1)]-V[\mbox{\boldmath$x$}(k)] < 0
\end{displaymath}](img294.png) |
(4.125) |
となれば、リアプノフ関数が次第に縮小することになる。
ゆえに、(4.126)式に(4.125),(4.124)式を代入すると
となる。したがって
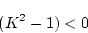 |
(4.127) |
のとき
![$\Delta V[\mbox{\boldmath$x$}(k)]$](img300.png) が負となり、安定となる。すなわち
が負となり、安定となる。すなわち
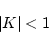 |
(4.128) |
が安定の条件である。
一般的にはリアプノフ関数を線形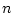 次の系では
次の系では
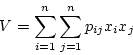 |
(4.129) |
ただし
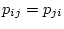
で実数
となり、正定の為には
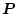 はシルベスタの条件
はシルベスタの条件
を満足しなければならない。



Next: 線形系の安定判別法
Up: 安定判別
Previous: 安定の概念
Yasunari SHIDAMA
平成15年6月30日
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-5-2.eps} \end{center} \end{figure}](img291.png)
![]() 次の系では
次の系では
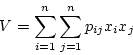
![$\displaystyle ただし\ \ \ \mbox{\boldmath$P$} = \left[ \begin{array}{cccc}
p_{1...
...dots & \ddots & \vdots \\
p_{1n} & \cdot & \cdots & p_{nn}
\end{array} \right]$](img306.png)