前章ではサンプリング信号を用いる制御系の理論について単入力、単出力という 古典制御理論的取扱いで述べた。
この章では、サンプリング制御系に状態空間の概念を導入し、多変数系としての 現代制御理論的取扱いについて述べる。通常このような場合、離散値系制御理論 といわれている。
一般に図4.1のようなサンプリング制御系のパルス伝達関数は次式のように分母分子![]() の多項式で表示される。
の多項式で表示される。
ただし、分子分母に共通の根がないものとする。例えば、
![]() の
場合、(4.1)式は次式となる。
の
場合、(4.1)式は次式となる。
| (4.2) |
いま1サンプリング遅延する要素を用いて上式をブロック線図で表示すると図
4.2のように表すことができる。![]() の要素が遅延要素を示して
いる。
の要素が遅延要素を示して
いる。
この図の
![]() を状態変数として考えると、図より
を状態変数として考えると、図より
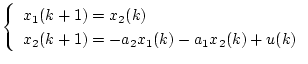 |
(4.4) | ||
![\begin{displaymath}
\begin{array}{l}
\left[
\begin{array}{l}
x_{1}(k+1) \\
x_{2...
...{array}{l}
x_{1}(k) \\
x_{2}(k)
\end{array}\right]
\end{array}\end{displaymath}](img26.png) |
(4.5) |
離散値系状態方程式を一般的に書くと、
![$\displaystyle \left[
\begin{array}{c}
x_{1}(k+1) \\
x_{2}(k+1) \\
\vdots \\
x_{n}(k+1)
\end{array}\right]$](img27.png) |
![$\displaystyle \left[
\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1n} \\
...
...egin{array}{c}
u_{1}(k) \\
u_{2}(k) \\
\vdots \\
u_{r}(k)
\end{array}\right]$](img29.png) |
(4.6) | |
![$\displaystyle \left[
\begin{array}{c}
y_{1}(k) \\
y_{2}(k) \\
\vdots \\
y_{m}(k)
\end{array}\right]$](img30.png) |
![$\displaystyle \left[
\begin{array}{cccc}
c_{11} & c_{12} & \cdots & c_{1n} \\
...
...n{array}{c}
x_{1}(k) \\
x_{2}(k) \\ \
\vdots \\
x_{n}(k)
\end{array}\right]$](img31.png) |
(4.7) |
| (4.8) | |||
| (4.9) |
| (4.10) | |||
| (4.11) |