Next: この文書について...
Up: 状態観測器(State Obserber)
Previous: 同形観測器
前項で述べた観測器はプラントと同次数を要するが、測定可能な状態変数は推定
する必要がないから、その分を除けば次数が下げられ、それだけ装置が簡単にな
る。このような観測器を低次元観測器という。
いまプラントの状態変数のうち測定不可能な変数を
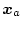 、また
、また
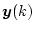 から直接測定可能な変数を
から直接測定可能な変数を
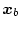 とする。このように分けて状態方程式を表
すと
とする。このように分けて状態方程式を表
すと
![\begin{displaymath}
\left[ \begin{array}{c}
\mbox{\boldmath$x$}_a(k+1) \\
\mb...
...ox{\boldmath$B$}_2
\end{array} \right] \mbox{\boldmath$u$}(k)
\end{displaymath}](img706.png) |
(4.326) |
![\begin{displaymath}
\mbox{\boldmath$y$}(k) = \left[ \begin{array}{cc}
\mbox{\bo...
...th$x$}_a(k) \\
\mbox{\boldmath$x$}_b(k)
\end{array} \right]
\end{displaymath}](img707.png) |
(4.327) |
となる。
いま、
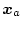 と
と
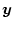 とより構成されるベクトルを
とより構成されるベクトルを
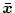 とすると
とすると
![\begin{displaymath}
\bar{\mbox{\boldmath$x$}} = \left[ \begin{array}{c}
\mbox{\...
...boldmath$x$}_a \\
\mbox{\boldmath$x$}_b
\end{array} \right]
\end{displaymath}](img709.png) |
(4.328) |
と表すことができる。ここで
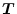 は変換行列で、
は変換行列で、
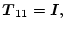
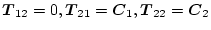 である。
この
である。
この
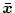 を用いて状態方程式を表すと
を用いて状態方程式を表すと
のようになる。ここで
である。
とすると、(4.330)式を分けて書けば
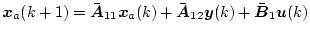 |
|
|
(4.331) |
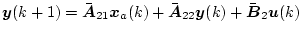 |
|
|
(4.332) |
とすると、(4.332)式のほうのみをモデルとして同形観測器を
構成した場合(4.318)式と同様に推定値は
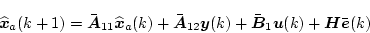 |
(4.333) |
となる。一方(4.333)式より
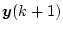 の推定値を書くと
の推定値を書くと
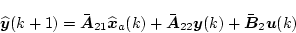 |
(4.334) |
となる。(4.334)
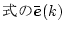 を
を
で定義した場合、(4.336)式を(4.334)式に代入すると
となる。
この観測器を示したのが図4.24である。しかしこの観測器には
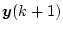 の入力が必要である。これは
の入力が必要である。これは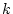 時点では未知であり、使用できない。
時点では未知であり、使用できない。
図 4.24:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-8-2.eps} \end{center} \end{figure}](img729.png) |
そこでいま
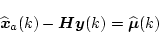 |
(4.337) |
とおくと
という式が得られる。また(4.338)式を書き直すと
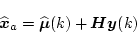 |
(4.339) |
となるから
![\begin{displaymath}
\widehat{\bar{\mbox{\boldmath$x$}}}(k)=
\left[ \begin{array}...
...ath$\mu$}}(k) \\
\mbox{\boldmath$y$}(k)
\end{array} \right]
\end{displaymath}](img740.png) |
(4.340) |
と表される。
(4.339)式の観測器を示したのが図4.25であり、この場合
は
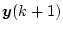 の入力を必要としない。
の入力を必要としない。
図 4.25:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-8-3.eps} \end{center} \end{figure}](img741.png) |
状態ベクトルの誤差を
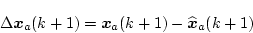 |
(4.341) |
で定義し、この式に(4.332)、(4.334)、(4.336)、
(4.333)、(4.335)式に代入すると
となる。この同時方程式の特性方程式は
![\begin{displaymath}
\det[Z\mbox{\boldmath$I$}-\bar{\mbox{\boldmath$A$}}_{11}+\mb...
...\mbox{\boldmath$A$}}_{21}]
=(Z-Z_1)(Z-Z_2)\cdots (Z-Z_{n-r})=0
\end{displaymath}](img749.png) |
(4.343) |
となり、この根が総て単位円のなかにあれば誤差は減衰をし、
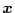 の推定値は
実際値に漸近する。
の推定値は
実際値に漸近する。
[例] 離散値系状態方程式が次のように与えられた場合の状態方程式を設計する。
この場合、直接測定できるのが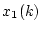 であり、できないのが
であり、できないのが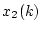 である
から、
である
から、
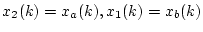 とすると
とすると
と書ける。この場合
となるので
となる。
(4.344)式に代入すると
となる。この根が単位円にはいるよう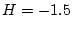 に選ぶと、
に選ぶと、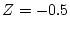 となり
(4.343)式は収束する。
となり
(4.343)式は収束する。
以上を図4.25に適用すると、低次元観測器は図4.26のようになる。
図 4.26:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-8-4.eps} \end{center} \end{figure}](img758.png) |
また(4.339)式に代入すると
となり、Z変換すると
となる。これを(4.340)式に代入すると
となる。一方与えられたシステムの伝達関数は次のようになる。
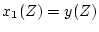 であるから、これを前式に代入すると
であるから、これを前式に代入すると
となり、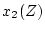 の伝達関数と等しくなるので状態観測器の役を果たしていること
がわかる。
の伝達関数と等しくなるので状態観測器の役を果たしていること
がわかる。



Next: この文書について...
Up: 状態観測器(State Obserber)
Previous: 同形観測器
Yasunari SHIDAMA
平成15年6月30日
![]() 、また
、また
![]() から直接測定可能な変数を
から直接測定可能な変数を
![]() とする。このように分けて状態方程式を表
すと
とする。このように分けて状態方程式を表
すと
![\begin{displaymath}
\left[ \begin{array}{c}
\mbox{\boldmath$x$}_a(k+1) \\
\mb...
...ox{\boldmath$B$}_2
\end{array} \right] \mbox{\boldmath$u$}(k)
\end{displaymath}](img706.png)
![\begin{displaymath}
\mbox{\boldmath$y$}(k) = \left[ \begin{array}{cc}
\mbox{\bo...
...th$x$}_a(k) \\
\mbox{\boldmath$x$}_b(k)
\end{array} \right]
\end{displaymath}](img707.png)
![]() と
と
![]() とより構成されるベクトルを
とより構成されるベクトルを
![]() とすると
とすると
![\begin{displaymath}
\bar{\mbox{\boldmath$x$}} = \left[ \begin{array}{c}
\mbox{\...
...boldmath$x$}_a \\
\mbox{\boldmath$x$}_b
\end{array} \right]
\end{displaymath}](img709.png)
![\begin{displaymath}
\bar{\mbox{\boldmath$A$}}=
\left[ \begin{array}{cc}
\bar...
...h$B$}}_1 \\
\bar{\mbox{\boldmath$B$}}_2
\end{array} \right]
\end{displaymath}](img716.png)
![]() の入力が必要である。これは
の入力が必要である。これは![]() 時点では未知であり、使用できない。
時点では未知であり、使用できない。
![\begin{displaymath}
\widehat{\bar{\mbox{\boldmath$x$}}}(k)=
\left[ \begin{array}...
...ath$\mu$}}(k) \\
\mbox{\boldmath$y$}(k)
\end{array} \right]
\end{displaymath}](img740.png)
![]() の入力を必要としない。
の入力を必要としない。
![\begin{eqnarray*}
\mbox{\boldmath$x$}(k+1) & = & \left[ \begin{array}{cc}
-2 &...
...in{array}{cc}
1 & 0
\end{array} \right] \mbox{\boldmath$x$}(k)
\end{eqnarray*}](img750.png)
![]() であり、できないのが
であり、できないのが![]() である
から、
である
から、
![]() とすると
とすると
![\begin{eqnarray*}
\left[ \begin{array}{c}
x_a(k+1) \\
x_b(k+1)
\end{array} ...
...\left[ \begin{array}{c}
x_a(k) \\
x_b(k)
\end{array} \right]
\end{eqnarray*}](img752.png)
![\begin{displaymath}
\mbox{\boldmath$T$}= \left[ \begin{array}{cc}
1 & 0 \\
0 & 1
\end{array} \right]
\end{displaymath}](img753.png)
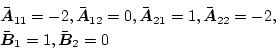
![\begin{displaymath}
\left[ \begin{array}{c}
x_1(Z) \\
x_2(Z)
\end{array} \ri...
... \left[ \begin{array}{c}
1 \\
Z+2
\end{array} \right] u(Z)
\end{displaymath}](img762.png)