


Next: Nested Programming
Up: 状態変数
Previous: 状態変数
サンプル値制御装置のように離散値信号のみで、すなわち連続信号を用いずに、
演算や信号変換を行う場合には、遅延要素のみで装置を構成することができる。
その一つの方法として、前例の場合のように1サンプリング遅延要素ごとに状態
変数をとるのが直接法である。
いまパルス伝達関数を一般的に
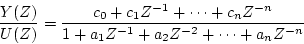 |
(4.12) |
で表したとき
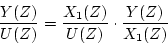 |
(4.13) |
とし、
とおくと、
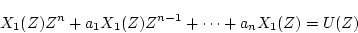 |
(4.16) |
となる。ここで
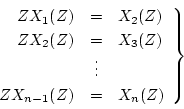 |
(4.17) |
とおくと、
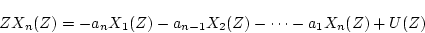 |
(4.18) |
となる。以上の式を逆Z変換すると、
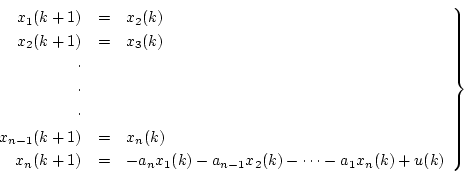 |
(4.19) |
となる。一方
となる。すなわち状態方程式としては
![\begin{displaymath}
\left[
\matrix{
x_1(k+1) \cr
x_2(k+1) \cr
\vdots \cr
x_...
...box{-1em}\vdots \cr
\makebox[0pt]{}\cr
1 \cr
}
\right]u(k)
\end{displaymath}](img54.png) |
(4.21) |
![\begin{displaymath}
y(k) = \left[
\matrix{
\overline{c}_n& \overline{c}_{n-1}&...
... \cr
x_2(k) \cr
\vdots \cr
x_n(k) \cr
}
\right] + c_0u(k)
\end{displaymath}](img55.png) |
(4.22) |
ただし、
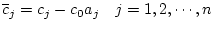
図 4.3:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-2-1.eps} \end{center} \end{figure}](img57.png) |
これは丁度連続系の相変換の場合に類似しており、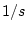 が
が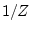 になっている形
である。
になっている形
である。
[例]
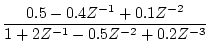 を直接法で表示する。
を直接法で表示する。
上式では
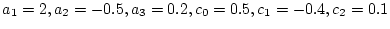 であるから状態方程式は次のようになる。
であるから状態方程式は次のようになる。
![\begin{displaymath}
\left[ \begin{array}{c}
x_1(k+1) \\
x_2(k+1) \\
x_3(k+1...
...[ \begin{array}{c}
0 \\
0 \\
1
\end{array} \right] u(k)
\end{displaymath}](img62.png) |
(4.23) |
![\begin{displaymath}
y(k) = \left[ \begin{array}{ccc}
-0.1& 0.35& -1.4
\end{ar...
...x_1(k) \\
x_2(k) \\
x_3(k)
\end{array} \right] + 0.5u(k)
\end{displaymath}](img64.png) |
(4.24) |
ブロック線図で描くと、図4.4のようになる。
図 4.4:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-2-2.eps} \end{center} \end{figure}](img65.png) |



Next: Nested Programming
Up: 状態変数
Previous: 状態変数
Yasunari SHIDAMA
平成15年6月30日
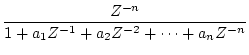
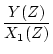
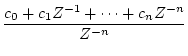
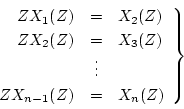
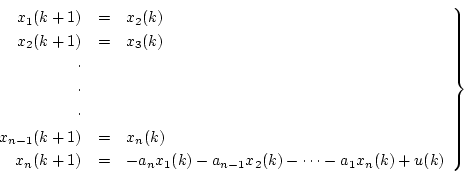
![\begin{displaymath}
\left[
\matrix{
x_1(k+1) \cr
x_2(k+1) \cr
\vdots \cr
x_...
...box{-1em}\vdots \cr
\makebox[0pt]{}\cr
1 \cr
}
\right]u(k)
\end{displaymath}](img54.png)
![\begin{displaymath}
y(k) = \left[
\matrix{
\overline{c}_n& \overline{c}_{n-1}&...
... \cr
x_2(k) \cr
\vdots \cr
x_n(k) \cr
}
\right] + c_0u(k)
\end{displaymath}](img55.png)
![]() が
が![]() になっている形
である。
になっている形
である。
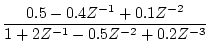 を直接法で表示する。
を直接法で表示する。
![]() であるから状態方程式は次のようになる。
であるから状態方程式は次のようになる。
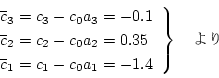
![\begin{displaymath}
y(k) = \left[ \begin{array}{ccc}
-0.1& 0.35& -1.4
\end{ar...
...x_1(k) \\
x_2(k) \\
x_3(k)
\end{array} \right] + 0.5u(k)
\end{displaymath}](img64.png)