


Next: 部分分数分解法(Diagonal Form)
Up: 状態変数
Previous: 直接法(Direct Programming)
(4.12)式を書き換えて
とすると
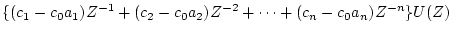 |
|
|
|
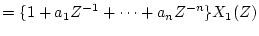 |
|
|
(4.26) |
となるから
と書き換え、両辺に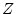 を掛けて
を掛けて
とおく。(4.28)式を逆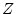 変換すると次式が得られる。
変換すると次式が得られる。
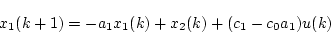 |
(4.29) |
次に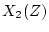 に
に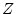 を掛けると、
を掛けると、
となり、これを逆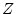 変換すると次式が得られる。
変換すると次式が得られる。
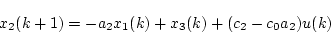 |
(4.31) |
以下同様にして
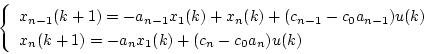 |
(4.32) |
となるので、一般的に状態方程式としては
![\begin{displaymath}
\left[
\begin{array}{c}
x_1(k+1) \\
x_2(k+1) \\
\vdot...
...
c_{n-1}-a_{n-1}c_0 \\
c_n-a_nc_0
\end{array} \right]u(k)
\end{displaymath}](img88.png) |
(4.33) |
![\begin{displaymath}
y(k) =
\left[
\matrix{1 & 0 & \cdots & 0}
\right]
\left...
...x_2(k) \\
\vdots \\
x_n(k)
\end{array} \right] + c_0u(k)
\end{displaymath}](img89.png) |
(4.34) |
がNested Programmingである。これをブロック線図に描くと図4.5となる。
図 4.5:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-2-3.eps} \end{center} \end{figure}](img90.png) |
[例]
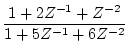 をNested Programmingで表示する。
をNested Programmingで表示する。
この場合
であるから
したがって状態方程式は次のようになる。
またブロック線図は図4.6のようになる。
図 4.6:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-2-4.eps} \end{center} \end{figure}](img96.png) |



Next: 部分分数分解法(Diagonal Form)
Up: 状態変数
Previous: 直接法(Direct Programming)
Yasunari SHIDAMA
平成15年6月30日
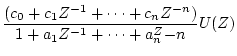
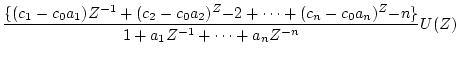
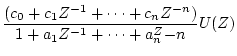
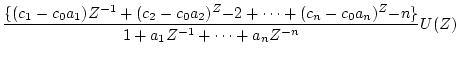
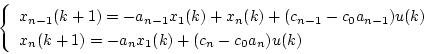
![\begin{displaymath}
\left[
\begin{array}{c}
x_1(k+1) \\
x_2(k+1) \\
\vdot...
...
c_{n-1}-a_{n-1}c_0 \\
c_n-a_nc_0
\end{array} \right]u(k)
\end{displaymath}](img88.png)
![\begin{displaymath}
y(k) =
\left[
\matrix{1 & 0 & \cdots & 0}
\right]
\left...
...x_2(k) \\
\vdots \\
x_n(k)
\end{array} \right] + c_0u(k)
\end{displaymath}](img89.png)
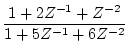 をNested Programmingで表示する。
をNested Programmingで表示する。
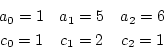
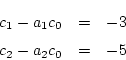
![\begin{displaymath}
\left[ \begin{array}{c}
x_1(k+1) \\
x_2(k+1)
\end{array}...
...
\left[ \begin{array}{c}
-3 \\
-5
\end{array} \right]u(k)
\end{displaymath}](img94.png)
![\begin{displaymath}
y(k) = \left[ \begin{array}{cc}
1 & 0
\end{array} \right]...
...gin{array}{c}
x_1(k) \\
x_2(k)
\end{array} \right] + u(k)
\end{displaymath}](img95.png)