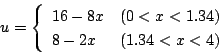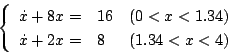Next: 一次遅れ系のオン・オフ制御
Up: 断片的線形化法
Previous: 断片的線形化法
断片的線形化法(Piece-wise Linear Method)とは、非線形特性を断片的に線形
化をし、その区間においては線形制御系として取り扱い、区間の切喚点において
は、前区間の最終条件をつぎの区間の初期条件としていく方法である。
制御要素の中に非線形特性が含まれている場合も通常は図5.19のように線形要素と
非線形要素に分離して取り扱う。この場合、制御方程式は
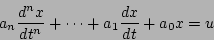 |
(5.74) |
と書かれるが、非線形要素が図5.20(a)の様なオン・オフ特性のときは
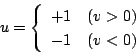 |
(5.75) |
となり、(b)のような飽和特性のときは
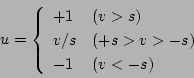 |
(5.76) |
となり、(c)図のような自乗特性のときは
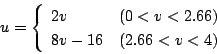 |
(5.77) |
となる。ただし、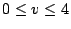 とする。
とする。
したがって、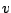 の値に応じて、それに対応する
の値に応じて、それに対応する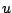 の値を用いた線形系として扱い、
の値を用いた線形系として扱い、
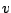 の値が次の区間に変わるとき、前の区間の最終条件を次の区間の初期条件と
して用いる。
の値が次の区間に変わるとき、前の区間の最終条件を次の区間の初期条件と
して用いる。
[例]自乗特性をもつ制御系
図5.21に示すような自乗特性をもつ制御系に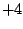 のステップ入力が加わったとする。
図より、
のステップ入力が加わったとする。
図より、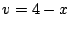 であるから、(5.79)式より
であるから、(5.79)式より
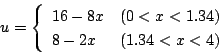 |
(5.78) |
となり、制御方程式は
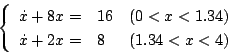 |
(5.79) |
となる。最初の区間では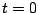 で
で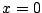 ゆえ
ゆえ
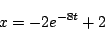 |
(5.80) |
となり、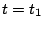 で
で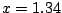 に達したとすれば
に達したとすれば
となる。これ以後次の区間に入るから、その区間の初期条件を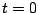 で
で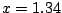 とすれば
とすれば
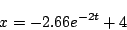 |
(5.81) |
となる。すなわち
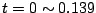 の間は(5.82)式の特性で、また
の間は(5.82)式の特性で、また
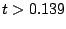 では(5.83)特性で表される。これを描いたのが図
5.22である。
では(5.83)特性で表される。これを描いたのが図
5.22である。



Next: 一次遅れ系のオン・オフ制御
Up: 断片的線形化法
Previous: 断片的線形化法
Yasunari SHIDAMA
平成15年7月28日
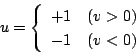
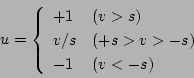
![]() の値に応じて、それに対応する
の値に応じて、それに対応する![]() の値を用いた線形系として扱い、
の値を用いた線形系として扱い、
![]() の値が次の区間に変わるとき、前の区間の最終条件を次の区間の初期条件と
して用いる。
の値が次の区間に変わるとき、前の区間の最終条件を次の区間の初期条件と
して用いる。