


Next: 多次系のオン・オフ制御
Up: 断片的線形化法
Previous: 概要
温度制御などには、装置の簡便さなどから、オンオフ制御が多く用いられる。そ
して通常このオン・オフ要素には多少ともヒステリシス特性をもっている。一方、
炉や恒温槽のような制御対象はむだ時間をもつ一次遅れ系として扱われる。この
制御系をブロック図で示すと図5.23のようになる。
制御方程式は
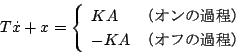 |
(5.82) |
で表される。いまステップ入力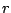 が加わった場合を考える。
が加わった場合を考える。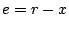 であるから、初期値
であるから、初期値 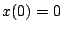 であれば
であれば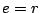 となる。(
となる。(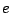 は今まで
の
は今まで
の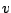 と同じである。)
と同じである。)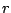 がヒステリシス幅
がヒステリシス幅 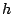 より充分大きければ
より充分大きければ
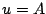 となる。図5.24に示すように、
となる。図5.24に示すように、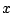 が
が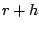 に到達する
まではこの状態が続く。ここで
に到達する
まではこの状態が続く。ここで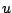 は
は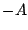 に切り換わる。しかしむだ時間がある
ため、その時点から
に切り換わる。しかしむだ時間がある
ため、その時点から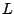 秒後までは
秒後までは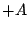 が加わっていたと同じ状態が継続される。
その点までは(5.84)式のオンの過程の式が用いられる。それから
が加わっていたと同じ状態が継続される。
その点までは(5.84)式のオンの過程の式が用いられる。それから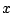 は下降を始め、
は下降を始め、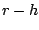 までは
までは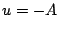 であり、そこで
であり、そこで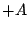 に切り換わるが、
前と同様
に切り換わるが、
前と同様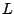 秒後までは
秒後までは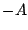 が加わっていたと同じ状態が続く。この間は
(5.84)式のオフの過程の式が用いられる。
が加わっていたと同じ状態が続く。この間は
(5.84)式のオフの過程の式が用いられる。
すなわち、まず最初の区間では、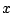 は(5.84)式のオンの過程の式の
解に
は(5.84)式のオンの過程の式の
解に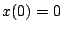 の条件を適用した
の条件を適用した
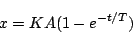 |
(5.83) |
の応答をする。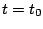 で
で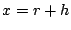 となる。
となる。
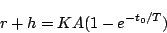 |
(5.84) |
また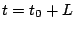 で、
で、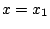 になったとすると
になったとすると
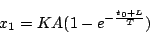 |
(5.85) |
となる。
次の区間は(5.84)式のオフの過程の式に初期値を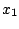 として解を求めると
として解を求めると
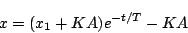 |
(5.86) |
となる。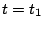 で
で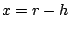 となるから
となるから
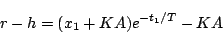 |
(5.87) |
となり、また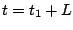 で
で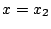 となるので
となるので
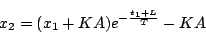 |
(5.88) |
となる。この式に(5.89)式を適用すると
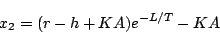 |
(5.89) |
さらに次の区間はオンの過程となり、このときは初期値を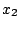 とする。その時の解は
とする。その時の解は
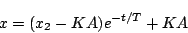 |
(5.90) |
であり、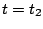 で
で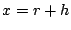 となるので
となるので
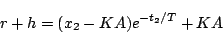 |
(5.91) |
となり、かつ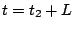 で
で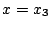 になるので
になるので
となる。以後同じことが繰り返される。
(5.94)式からわかるように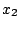 も
も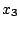 も、
も、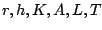 に
よって定まる値であるから
に
よって定まる値であるから
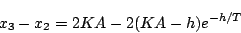 |
(5.93) |
がリミットサイクルの振幅となる。
一方、リミットサイクルのときは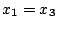 であるから、(5.94)式の
であるから、(5.94)式の
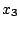 を(5.89)式の
を(5.89)式の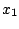 のところに代入すると
のところに代入すると
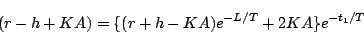 |
(5.94) |
となるから
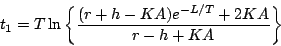 |
(5.95) |
となる。同様にして(5.91)式と(5.93)式より
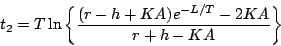 |
(5.96) |
が得られるので、リミットサイクルの同期は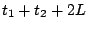 となる。
となる。



Next: 多次系のオン・オフ制御
Up: 断片的線形化法
Previous: 概要
Yasunari SHIDAMA
平成15年7月28日
![\includegraphics[scale=0.60]{eps/5-3-5.eps}](img278.png)
![]() は(5.84)式のオンの過程の式の
解に
は(5.84)式のオンの過程の式の
解に![]() の条件を適用した
の条件を適用した
![]() として解を求めると
として解を求めると
![]() も
も![]() も、
も、![]() に
よって定まる値であるから
に
よって定まる値であるから
![]() であるから、(5.94)式の
であるから、(5.94)式の
![]() を(5.89)式の
を(5.89)式の![]() のところに代入すると
のところに代入すると