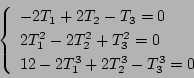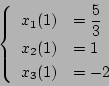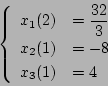

Next: 状態面及び位相面解析
Up: 断片的線形化法
Previous: 多次系のオン・オフ制御
目標値に最短で到達させるには、オン・オフ制御が用いられる。たとえば二次系
の場合、最初最大のエネルギーを加えて作動させ、次にある時点で逆方向に最大
のエネルギーを加えて制動させ、丁度目標値で停止させ、そこでエネルギーを切
れば、それが最短時間で目標値に到達する制御になる。
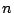 次系の場合は、図5.28のように
次系の場合は、図5.28のように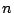 回オン・オフの切換えを必要
とする。ただし、最後の切り換えは入力を停止するためのものである。
回オン・オフの切換えを必要
とする。ただし、最後の切り換えは入力を停止するためのものである。
図5.28の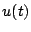 を式の形で表すと次のようになる。
を式の形で表すと次のようになる。
![\begin{displaymath}
U(s)= \frac{\pm 1}{s} \left[ 1-2e^{-sT_1}+2e^{-sT_2}- \cdots
+2(-1)^{n-1}e^{-sT_{n-1}}+(-1)^ne^{-sT_n}
\right]
\end{displaymath}](img374.png) |
(5.120) |
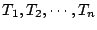 は切換え時点を示している。最初の正負の符号は目標値、
または初期値によって決定される。
は切換え時点を示している。最初の正負の符号は目標値、
または初期値によって決定される。
制御対象は1型以上の特性(一つ以上の積分特性)を持つものとし、かつ
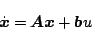 |
(5.121) |
という単入力系とする。上式を初期値を考慮してラプラス変換すると
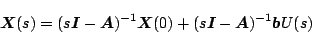 |
(5.122) |
となる。この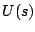 に(5.122)式を代入すればオン・オフ制御による
各変数の応答が得られる。
に(5.122)式を代入すればオン・オフ制御による
各変数の応答が得られる。
いま各変数のうち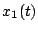 のみを目標値に到達させ、他の変数は目標値で制止さ
せる場合を考える。この場合座標のとり方により初期値を与え、目標値を原点に
とるようにしても同じである。
のみを目標値に到達させ、他の変数は目標値で制止さ
せる場合を考える。この場合座標のとり方により初期値を与え、目標値を原点に
とるようにしても同じである。
そこで、(5.124)式中の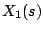 が完全関数(Entire Function)となる
ように、すなわち
が完全関数(Entire Function)となる
ように、すなわち および
および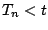 で0となるようにする。
で0となるようにする。
これを式で表現すると
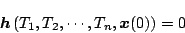 |
(5.123) |
となる。ただし
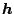 はベクトル関数を意味する。このためには
はベクトル関数を意味する。このためには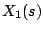 の各
極に対する留数を0にすればよい。このことは
の各
極に対する留数を0にすればよい。このことは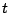 の上記範囲に対応する複素面
上の領域に極がないことを意味している。
の上記範囲に対応する複素面
上の領域に極がないことを意味している。
初期値
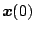 から
から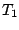 時間後に最初のオン・オフの切換えが行われる。
この時の各状態量を
時間後に最初のオン・オフの切換えが行われる。
この時の各状態量を
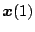 とすると、これが最適切換えのための切換空
間
とすると、これが最適切換えのための切換空
間
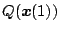 である。任意の初期値から出発しても、必ずこの切換え空
間で切換えれば最短時間制御が行える。この切換え以後に関しては
である。任意の初期値から出発しても、必ずこの切換え空
間で切換えれば最短時間制御が行える。この切換え以後に関しては
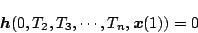 |
(5.124) |
が成立するようにする。
以下同様にして、(5.125)、(5.126)式のような状件をたて、
それから、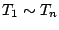 が決定される。
が決定される。
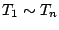 が決定されると切換空間
が決定されると切換空間
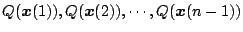 が求められる。
が求められる。
[例1]サーボ系の場合
制御対象の状態方程式が
![\begin{displaymath}
\dot{ \mbox{\boldmath$x$} }=
\left[
\begin{array}{cc}
0 ...
...} +
\left[
\begin{array}{c}
0 \\
1
\end{array} \right] u
\end{displaymath}](img392.png) |
(5.125) |
で与えられたとする。これを(5.124)式に適用すると
![\begin{displaymath}
\mbox{\boldmath$X$} (s) =
\frac {1}{s(s+1)}
\left[
\begi...
...
\left[
\begin{array}{c}
1 \\
s
\end{array} \right] U(s)
\end{displaymath}](img393.png) |
(5.126) |
となる。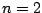 であり、最初の
であり、最初の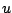 を
を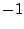 とする事が必要な場合とすると
(5.122)式より
とする事が必要な場合とすると
(5.122)式より
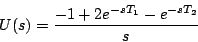 |
(5.127) |
となるので、これを(5.128)式に適用し、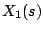 を求めると、
を求めると、
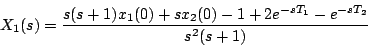 |
(5.128) |
となる。この関数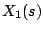 は
は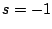 に1つの、また
に1つの、また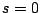 に2つの極を有する。
に2つの極を有する。
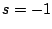 における留数は単根ゆえ、その場合の留数を求める法則
における留数は単根ゆえ、その場合の留数を求める法則
![\begin{displaymath}
R(s_0)=[(s-s_0)F(s)]_{s=s_0}
\end{displaymath}](img400.png) |
(5.129) |
に適用すると
となる。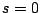 における留数は2乗根であるから
における留数は2乗根であるから
![\begin{displaymath}
R(s_0)= \frac{1}{(m-1)!} \left[ \frac{\mathrm{d}^{m-1}}{\mathrm{d}s^{m-1}} (s-s_0)^m F(s)
\right] _s=s_0
\end{displaymath}](img405.png) |
(5.131) |
(ただし、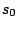 は
は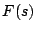 の
の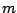 乗根)の法則に適用すると
乗根)の法則に適用すると
となる。したがって、(5.105)式は
![\begin{displaymath}
\mbox{\boldmath$h$} (T_1,T_2,\mbox{\boldmath$x$}(0))=
\lef...
...t]
=
\left[
\begin{array}{c}
0 \\
0
\end{array} \right]
\end{displaymath}](img414.png) |
(5.133) |
となり、これが完全関数のための条件となる。
切換え以後に関しては、上式の
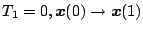 として
(5.106)式に代入すると
として
(5.106)式に代入すると
![\begin{displaymath}
\mbox{\boldmath$h$} (0,T_2,\mbox{\boldmath$x$}(1))=
\left[...
...t]
=
\left[
\begin{array}{c}
0 \\
0
\end{array} \right]
\end{displaymath}](img416.png) |
(5.134) |
となる。この式から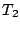 を消去すると
を消去すると
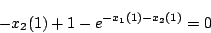 |
(5.135) |
が得られる。これが切換空間
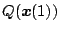 である。すなわち
である。すなわち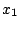 と
と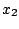 が上記条件を満足しているところで切換えると最短時間で原点に到達する。
(5.137)式を書き直すと
が上記条件を満足しているところで切換えると最短時間で原点に到達する。
(5.137)式を書き直すと
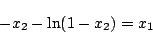 |
(5.136) |
となり、これが切換曲線を表している。
最初の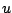 が
が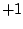 のときは
のときは
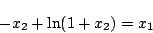 |
(5.137) |
が切換曲線となる。
[例2]3次積分系の場合
制御対象が
![\begin{displaymath}
\dot {\mbox{\boldmath$x$} } =
\left[
\begin{array}{ccc}
...
...eft[
\begin{array}{c}
0 \\
0 \\
1
\end{array} \right] u
\end{displaymath}](img422.png) |
(5.138) |
の3次積分系の場合で、最初の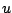 が
が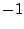 の場合
の場合
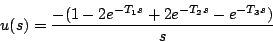 |
(5.139) |
となるので
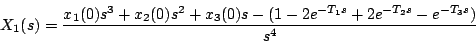 |
(5.140) |
と書き表せる。
この場合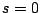 の4重根である。(5.142)式を(5.133)式に適
用し、
の4重根である。(5.142)式を(5.133)式に適
用し、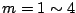 にとり、それを0とおく。
にとり、それを0とおく。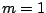 のときは両辺とも0となって
しまうので、その他の部分を記載すると
のときは両辺とも0となって
しまうので、その他の部分を記載すると
![\begin{displaymath}
\mbox{\boldmath$h$}(T_1,T_2,T_3,\mbox{\boldmath$x$} (0)) =
...
...\left[
\begin{array}{c}
0 \\
0 \\
0
\end{array} \right]
\end{displaymath}](img427.png) |
(5.141) |
となる。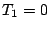 として
として
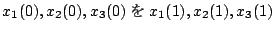 に書き換えると
に書き換えると
![\begin{displaymath}
\mbox{\boldmath$h$}(0,T_2,T_3,\mbox{\boldmath$x$} (1)) =
\...
...\left[
\begin{array}{c}
0 \\
0 \\
0
\end{array} \right]
\end{displaymath}](img430.png) |
(5.142) |
となり、さらに、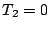 とし、
とし、
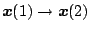 と書き換えると
と書き換えると
![\begin{displaymath}
\mbox{\boldmath$h$}(0,0,T_3,\mbox{\boldmath$x$} (2)) =
\le...
...\left[
\begin{array}{c}
0 \\
0 \\
0
\end{array} \right]
\end{displaymath}](img433.png) |
(5.143) |
となる。この式より、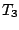 を消去し、切換空間
を消去し、切換空間
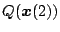 を求めると
を求めると
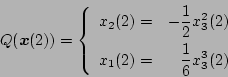 |
(5.144) |
となる。(5.144)式より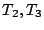 を消去すると切換空間
を消去すると切換空間
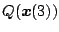 が得られる。この式は大部複雑な式となる。
が得られる。この式は大部複雑な式となる。
もし初期値が、
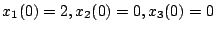 のように与えられると、
(5.143)式にこの値を代入し
のように与えられると、
(5.143)式にこの値を代入し
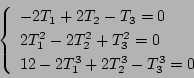 |
(5.145) |
これより
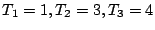 が得られる。
が得られる。
したがって、この値を(5.144)式に代入すると最初の切換えは
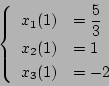 |
(5.146) |
のところであり、(5.145)式に代入すると、第2の切換えは
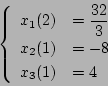 |
(5.147) |
のところになる。


Next: 状態面及び位相面解析
Up: 断片的線形化法
Previous: 多次系のオン・オフ制御
Yasunari SHIDAMA
平成15年7月28日
![]() 次系の場合は、図5.28のように
次系の場合は、図5.28のように![]() 回オン・オフの切換えを必要
とする。ただし、最後の切り換えは入力を停止するためのものである。
回オン・オフの切換えを必要
とする。ただし、最後の切り換えは入力を停止するためのものである。
![]() を式の形で表すと次のようになる。
を式の形で表すと次のようになる。
![]() のみを目標値に到達させ、他の変数は目標値で制止さ
せる場合を考える。この場合座標のとり方により初期値を与え、目標値を原点に
とるようにしても同じである。
のみを目標値に到達させ、他の変数は目標値で制止さ
せる場合を考える。この場合座標のとり方により初期値を与え、目標値を原点に
とるようにしても同じである。
![]() が完全関数(Entire Function)となる
ように、すなわち
が完全関数(Entire Function)となる
ように、すなわち![]() および
および![]() で0となるようにする。
で0となるようにする。
![]() から
から![]() 時間後に最初のオン・オフの切換えが行われる。
この時の各状態量を
時間後に最初のオン・オフの切換えが行われる。
この時の各状態量を
![]() とすると、これが最適切換えのための切換空
間
とすると、これが最適切換えのための切換空
間
![]() である。任意の初期値から出発しても、必ずこの切換え空
間で切換えれば最短時間制御が行える。この切換え以後に関しては
である。任意の初期値から出発しても、必ずこの切換え空
間で切換えれば最短時間制御が行える。この切換え以後に関しては
![]() が決定される。
が決定される。
![]() が決定されると切換空間
が決定されると切換空間
![]() が求められる。
が求められる。
![\begin{displaymath}
\dot{ \mbox{\boldmath$x$} }=
\left[
\begin{array}{cc}
0 ...
...} +
\left[
\begin{array}{c}
0 \\
1
\end{array} \right] u
\end{displaymath}](img392.png)
![$\displaystyle \left[ \frac{s(s+1)x_1(0)+sx_2(0)-1+2e^{-sT_1}
-e^{-sT_2}}{s^2} \right] _{s=-1}$](img403.png)
![$\displaystyle \frac{1}{(2-1)!} \left[ \frac{\mathrm{d}}{\mathrm{d}s} \frac{s(s+1)x_1(0)
+sx_2(0)-1+2e^{-sT_1}-e^{-sT_2}}{(s+1)}
\right] _{s=0}$](img410.png)
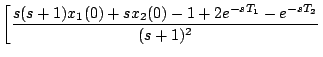
![$\displaystyle \left. - \frac{(2s+1)x_1(0) +x_2(0)-1-2T_1e^{-sT_1}+T_2e^{-sT_2}
}{(s+1)^2} \right] _{s=0}$](img412.png)
![\begin{displaymath}
\mbox{\boldmath$h$} (T_1,T_2,\mbox{\boldmath$x$}(0))=
\lef...
...t]
=
\left[
\begin{array}{c}
0 \\
0
\end{array} \right]
\end{displaymath}](img414.png)
![]() として
(5.106)式に代入すると
として
(5.106)式に代入すると
![\begin{displaymath}
\mbox{\boldmath$h$} (0,T_2,\mbox{\boldmath$x$}(1))=
\left[...
...t]
=
\left[
\begin{array}{c}
0 \\
0
\end{array} \right]
\end{displaymath}](img416.png)
![]() が
が![]() のときは
のときは
![\begin{displaymath}
\dot {\mbox{\boldmath$x$} } =
\left[
\begin{array}{ccc}
...
...eft[
\begin{array}{c}
0 \\
0 \\
1
\end{array} \right] u
\end{displaymath}](img422.png)
![]() の4重根である。(5.142)式を(5.133)式に適
用し、
の4重根である。(5.142)式を(5.133)式に適
用し、![]() にとり、それを0とおく。
にとり、それを0とおく。![]() のときは両辺とも0となって
しまうので、その他の部分を記載すると
のときは両辺とも0となって
しまうので、その他の部分を記載すると
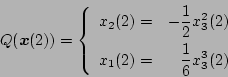
![]() のように与えられると、
(5.143)式にこの値を代入し
のように与えられると、
(5.143)式にこの値を代入し