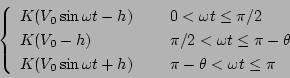Next: 記述関数法による安定判別
Up: 記述関数法(Describing Function)
Previous: 記述関数法(Describing Function)
図5.3(a)に示すように、非線形要素に正弦波入力を加えた場合、
出力波形は正弦波ではなく形が歪むが、入力と同じ同期を持つ周期的な波形となる。
したがって基本波およびその高周波数成分から構成されていると見なされる。
通常制御系の各種要素は高い周波数ではゲインが減衰する特性を有するから、
非線形要素と結合して使用されるときは高調波成分は減衰され無視できると考える。
そこで出力の基本成分のみを考え、これを(b)図に示すように等価出力とする。
その場合入力と出力は共に同じ周期の正弦波となるから、両者の間の関係は
等価線形化された要素と見なされ、これを記述関数(又は等価伝達関数)という。
いま非線形要素に加わる入力を
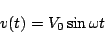 |
(5.18) |
の正弦波とし、出力波形をフーリエ級数で表示すると、次のようになる。
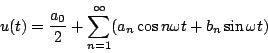 |
(5.19) |
出力波形が正負対称であれば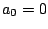 となる。基本波形成分のみを考えると
となる。基本波形成分のみを考えると
ただし
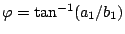
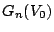 のゲインと位相は
のゲインと位相は
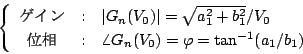 |
(5.21) |
で定義される。
[例1]ヒステリシスにある2位置リレー要素
図5.4に示すような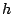 の幅のヒステリシスを持つ2位置リレー要素に、
正弦波の入力を加えると図5.5に示すように入力が
の幅のヒステリシスを持つ2位置リレー要素に、
正弦波の入力を加えると図5.5に示すように入力が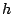 に達したところで
オン・オフが切り換り、出力は方形波状になる。
に達したところで
オン・オフが切り換り、出力は方形波状になる。
この基本成分の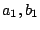 を(5.19)式より求めると
を(5.19)式より求めると
となる。したがって記述関数のゲイン及び位相は次のようになる。
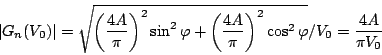 |
(5.24) |
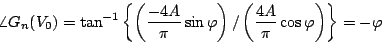 |
(5.25) |
この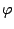 は図5.5より
は図5.5より
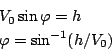 |
(5.26) |
の関係があることがわかる。
この例からもわかるように記述関数のゲインも位相も入力正弦波の振幅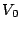 の
関数となっている。
の
関数となっている。
[例2]ヒステリシスのある3位置リレー要素
図5.6に示すようなヒステリシスのある3位置リレーの場合
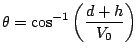 |
|
|
(5.27) |
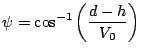 |
|
|
(5.28) |
とすると図5.7より
となる。これより記述関数のゲインと位相を求めると
となる。
図 5.7:
![\includegraphics[scale=0.60]{eps/5-2-5.eps}](img92.png)
j
|
[例3]バックラッシュ(ヒステリシス)要素
図5.8に示すようなバックラッシュ要素の場合、正弦波入力に対する
出力波形は図5.9のようになる。
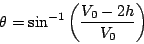 |
(5.33) |
とした場合、出力は
となるので
となり、これを(5.21)式に代入してゲインおよび位相が求められる。
飽和要素
ただし
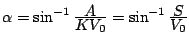
不感帯要素
ただし
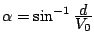



Next: 記述関数法による安定判別
Up: 記述関数法(Describing Function)
Previous: 記述関数法(Describing Function)
Yasunari SHIDAMA
平成15年7月28日
![\includegraphics[scale=0.60]{eps/5-2-1.eps}](img42.png)
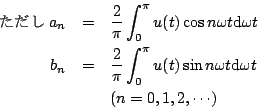
![]() となる。基本波形成分のみを考えると
となる。基本波形成分のみを考えると
![]() の幅のヒステリシスを持つ2位置リレー要素に、
正弦波の入力を加えると図5.5に示すように入力が
の幅のヒステリシスを持つ2位置リレー要素に、
正弦波の入力を加えると図5.5に示すように入力が![]() に達したところで
オン・オフが切り換り、出力は方形波状になる。
に達したところで
オン・オフが切り換り、出力は方形波状になる。
![]() を(5.19)式より求めると
を(5.19)式より求めると
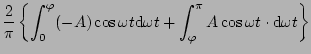
![$\displaystyle \frac{2A}{\pi} \{ [-\sin \omega t]_0^{\varphi}
+[\sin \omega t]_{\varphi} ^{\pi} \}$](img59.png)
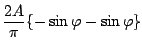
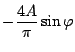
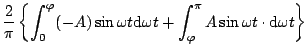
![$\displaystyle \frac{2A}{\pi} \{ [\cos \omega t]_0^{\varphi}
-[\cos \omega t]_{\varphi} ^{\pi} \}$](img64.png)
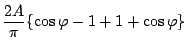
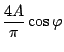
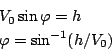
![]() の
関数となっている。
の
関数となっている。
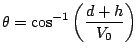
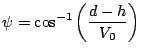
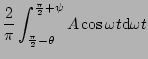
![$\displaystyle \frac{2A}{\pi} \left[ \sin \left( \frac{\pi}{2}+\psi \right)
-\sin \left( \frac{\pi}{2}-\theta \right) \right]$](img75.png)
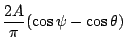
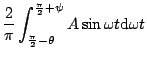
![$\displaystyle \frac{2A}{\pi} \left[ -\cos \left( \frac{\pi}{2}+\psi \right)
+\cos \left( \frac{\pi}{2}-\theta \right) \right]$](img78.png)