

Next: この文書について...
Up: 計算機シミュレーション
Previous: 各方法の比較
前述のごとく、状態遷移法によってシミュレーションを行う場合一般に
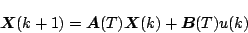 |
(7.52) |
の形で取り扱うのであるが、この式が図7.2のように、サンプリングと
ホールドを通して制御対象を駆動するときには、(7.52)式を
同次方程式に変換して取り扱うことができる。
これを例によって示す。いま制御対象の伝達関数を
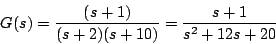 |
(7.53) |
とし、これをNested Programmingで表示すると、
![\begin{displaymath}
\left[ \begin{array}{c}
\dot{x}_1 \\
\dot{x}_2
\end{arra...
... +
\left[ \begin{array}{c}
1 \\
1
\end{array} \right] m(t)
\end{displaymath}](img117.png) |
(7.54) |
となる。ここ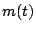 ではサンプリングをホールドしたものであるから、断片的に
一定値である。したがって
ではサンプリングをホールドしたものであるから、断片的に
一定値である。したがって
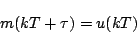 |
(7.55) |
但し
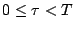
これは、図7.3に示すごとく、積分器の入力が0で初期値が
各サンプリング時点において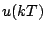 であるのと等価的に考えられる。
このように考えてシステムのブロックダイヤグラムを描くと図7.4の
ようになる。
であるのと等価的に考えられる。
このように考えてシステムのブロックダイヤグラムを描くと図7.4の
ようになる。
この図の状態方程式は次のように書くことができる。
![\begin{displaymath}
\left[ \begin{array}{c}
\dot{m} \\
\dot{x}_1 \\
\dot{x}...
...ft[ \begin{array}{c}
m \\
x_1 \\
x_2
\end{array} \right]
\end{displaymath}](img125.png) |
(7.56) |
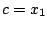
但し、
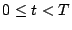
したがって初期値を
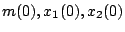 としたとき、
としたとき、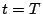 のときでは
のときでは
![\begin{displaymath}
\left[ \begin{array}{c}
m(T) \\
x_1(T) \\
x_2(T)
\end{...
...n{array}{c}
u(0) \\
x_1(0) \\
x_2(0)
\end{array} \right]
\end{displaymath}](img130.png) |
(7.57) |
ここで
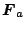 は
は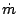 を含めたシステム方程式のシステムマトリックス
である。この結果から一般的に
を含めたシステム方程式のシステムマトリックス
である。この結果から一般的に
![\begin{displaymath}
\left[ \begin{array}{c}
m(k+1) \\
x_1(k+1) \\
x_2(k+1)
...
...n{array}{c}
u(k) \\
x_1(k) \\
x_2(k)
\end{array} \right]
\end{displaymath}](img133.png) |
(7.58) |
として表すことができる。この式は同次方程式であり、この式を用いて
シミュレーションをすれば指数項の計算が少なくてすむ利点がある。この場合
![\begin{displaymath}
\mbox{\boldmath$F$}_a = \left[ \begin{array}{cc}
0 & 0 \\
\mbox{\boldmath$G$} & \mbox{\boldmath$F$}
\end{array} \right]
\end{displaymath}](img135.png) |
(7.59) |
より求められる。
次に離散値系のシミュレーションに際し、サンプリング時点間の挙動を見る
方法について述べる。
いまサンプリング同期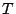 に対して、その間の任意の等分時間を
に対して、その間の任意の等分時間を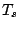 とし
とし
 |
(7.60) |
とおいたとき、サンプリング時点間の挙動は、例えば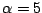 の場合
の場合
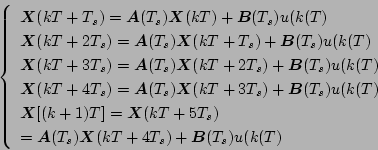 |
(7.61) |
より求められる。
これを同次方程式に変換して求めるときは
![\begin{displaymath}
\left\{ \begin{array}{l}
\left[ \begin{array}{c}
m(kT+T_s...
...oldmath$X$}(kT+4T_s)
\end{array} \right]
\end{array} \right.
\end{displaymath}](img140.png) |
(7.62) |
の式を用いる。


Next: この文書について...
Up: 計算機シミュレーション
Previous: 各方法の比較
Yasunari SHIDAMA
平成15年7月29日
![\begin{displaymath}
\left[ \begin{array}{c}
\dot{x}_1 \\
\dot{x}_2
\end{arra...
... +
\left[ \begin{array}{c}
1 \\
1
\end{array} \right] m(t)
\end{displaymath}](img117.png)
![]() であるのと等価的に考えられる。
このように考えてシステムのブロックダイヤグラムを描くと図7.4の
ようになる。
であるのと等価的に考えられる。
このように考えてシステムのブロックダイヤグラムを描くと図7.4の
ようになる。
![\begin{displaymath}
\left[ \begin{array}{c}
\dot{m} \\
\dot{x}_1 \\
\dot{x}...
...ft[ \begin{array}{c}
m \\
x_1 \\
x_2
\end{array} \right]
\end{displaymath}](img125.png)
![\begin{displaymath}
\left[ \begin{array}{c}
m(T) \\
x_1(T) \\
x_2(T)
\end{...
...n{array}{c}
u(0) \\
x_1(0) \\
x_2(0)
\end{array} \right]
\end{displaymath}](img130.png)
![\begin{displaymath}
\left[ \begin{array}{c}
m(k+1) \\
x_1(k+1) \\
x_2(k+1)
...
...n{array}{c}
u(k) \\
x_1(k) \\
x_2(k)
\end{array} \right]
\end{displaymath}](img133.png)
![\begin{displaymath}
\mbox{\boldmath$F$}_a = \left[ \begin{array}{cc}
0 & 0 \\
\mbox{\boldmath$G$} & \mbox{\boldmath$F$}
\end{array} \right]
\end{displaymath}](img135.png)
![]() に対して、その間の任意の等分時間を
に対して、その間の任意の等分時間を![]() とし
とし
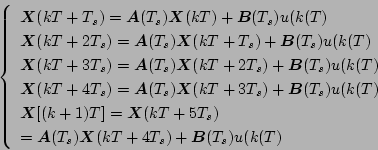
![\begin{displaymath}
\left\{ \begin{array}{l}
\left[ \begin{array}{c}
m(kT+T_s...
...oldmath$X$}(kT+4T_s)
\end{array} \right]
\end{array} \right.
\end{displaymath}](img140.png)