

Next: 状態遷移法によるシミュレーション
Up: 計算機シミュレーション
Previous: 状態遷移法
以上の各方法のついて比較すると、同一のきざみ幅に対して
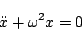 |
(7.51) |
の、ある発振回路の所要計算時間を比較すると、
| Runge-Kutta |
Euler |
Tustin |
状態方程式 |
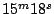 |
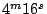 |
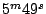 |
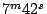 |
という具合である。精度は
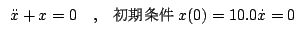 について、
について、
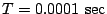 で求めた場合は7.1表のごとく何れの方法で
も殆ど同じである。
で求めた場合は7.1表のごとく何れの方法で
も殆ど同じである。
表 7.1:
| 時間 |
Runge-Kutta |
Euler |
Tustin |
状態方程式 |
| 1 |
5.403 |
5.403 |
5.403 |
5.403 |
| 2 |
-4.161 |
-4.161 |
-4.161 |
-4.160 |
| 3 |
-9.898 |
-9.900 |
-9.897 |
-9.896 |
| 3.14 |
-9.998 |
-10.00 |
-9.997 |
-9.996 |
| 4 |
-6.536 |
-6.536 |
-6.534 |
-6.533 |
| 5 |
2.836 |
2.836 |
2.835 |
2.835 |
| 6 |
9.598 |
9.601 |
9.596 |
9.594 |
| 6.28 |
9.996 |
9.999 |
9.994 |
9.991 |
| 7 |
7.536 |
7.539 |
7.534 |
7.532 |
| 8 |
-1.454 |
-1.455 |
-1.454 |
-1.454 |
| 9 |
-9.106 |
-9.111 |
-9.104 |
-9.100 |
つぎに
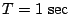 のきざみ幅で求めると、7.2表のごとくなり、
とくにEulerの方法は不安定となり誤差が非常に大きくなる。他の3方法は
安定ではあるが、状態方程式の方法が最も誤差が少ない。但しこの場合
のきざみ幅で求めると、7.2表のごとくなり、
とくにEulerの方法は不安定となり誤差が非常に大きくなる。他の3方法は
安定ではあるが、状態方程式の方法が最も誤差が少ない。但しこの場合
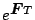 の精度を
の精度を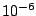 以内にしてある。
以内にしてある。
表 7.2:
| 時間 |
Runge-Kutta |
Euler |
Tustin |
状態方程式 |
| 1 |
5.417 |
10.000 |
6.0 |
5.403 |
| 2 |
-4.010 |
0 |
-2.8 |
-4.161 |
| 3 |
-9.695 |
-20 |
-9.36 |
-9.900 |
| 4 |
-6.542 |
-40 |
-8.432 |
-6.536 |
| 5 |
2.491 |
-40 |
-7.584 |
2.837 |
| 6 |
9.161 |
0 |
7.522 |
9.602 |
| 7 |
7.463 |
80 |
9.785 |
7.540 |
| 8 |
-9.638 |
160 |
4.220 |
-1.455 |
| 9 |
-8.417 |
160 |
-4.721 |
-9.111 |
| 10 |
-8.166 |
0 |
-9.885 |
-8.40 |


Next: 状態遷移法によるシミュレーション
Up: 計算機シミュレーション
Previous: 状態遷移法
Yasunari SHIDAMA
平成15年7月29日
![]() のきざみ幅で求めると、7.2表のごとくなり、
とくにEulerの方法は不安定となり誤差が非常に大きくなる。他の3方法は
安定ではあるが、状態方程式の方法が最も誤差が少ない。但しこの場合
のきざみ幅で求めると、7.2表のごとくなり、
とくにEulerの方法は不安定となり誤差が非常に大きくなる。他の3方法は
安定ではあるが、状態方程式の方法が最も誤差が少ない。但しこの場合
![]() の精度を
の精度を![]() 以内にしてある。
以内にしてある。