


Next: ホロノミックな拘束と非ホロノミックな拘束の性質
Up: ホロノミックと非ホロノミックシステム
Previous: ホロノミックと非ホロノミックシステム
Contents
ホロノミック,非ホロノミックとは力学的拘束を分類した用語である.ホロノミックな拘束とは拘束条件が一般化座標と時間のみに依存する方程式によって解析的に表現できるものである.それ以外の拘束はすべて非ホロノミックな拘束と呼ばれる.
ホロノミックな拘束とは一般化座標を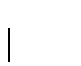 ,時間を
,時間を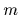 としたときに次のように表される拘束をいう.
としたときに次のように表される拘束をいう.
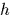 |
(89) |
ここで,関数はすべて解析的であるものとする.今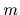 とし,
とし,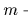 の
の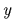 に関するヤコビ行列はフルランクであると仮定する.これは(A.1)式に含まれる
に関するヤコビ行列はフルランクであると仮定する.これは(A.1)式に含まれる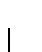 個の式が独立であることを意味する.陰関数定理によれば,この場合(A.1)式を用いて
個の式が独立であることを意味する.陰関数定理によれば,この場合(A.1)式を用いて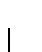 個の一般化座標を解くことができる.この低次元化によって,システム全体の挙動を拘束する条件を持たない
個の一般化座標を解くことができる.この低次元化によって,システム全体の挙動を拘束する条件を持たない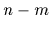 個の独立な一般化座標で記述できる.
さて,拘束条件が(A.1)式のような代数方程式でなく
個の独立な一般化座標で記述できる.
さて,拘束条件が(A.1)式のような代数方程式でなく
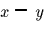 |
(90) |
のような微分方程式で表されることがある.もし(A.2)式が(A.1)式のような形式に帰着できるならば,その拘束は積分可能であるという.この時当然,拘束はホロノミックである.(A.2)式が(A.1)式の形式に帰着できないとき,拘束は積分不可能で,非ホロノミックとなる.拘束がホロノミックな場合には,拘束条件を用いて一般化座標の一部を消去し低次元化をはかることができる.
一般化座標の数から独立な拘束条件の数を引いたものが「自由度」である.したがって(A.1)式も(A.2)式もm個の独立な式からなるとすると,(A.1)式で低次元化されたシステムも(A.2)式を拘束条件とするシステムも共にシステムの自由度は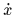 となる.一方,一般化座標の数は前者で
となる.一方,一般化座標の数は前者で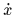 ,後者でnである.通常の移動ロボットでは一般化座標の数(駆動軸数)と自由度数はほとんど同義語になっていることと対比される.
,後者でnである.通常の移動ロボットでは一般化座標の数(駆動軸数)と自由度数はほとんど同義語になっていることと対比される.
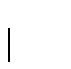 平面上に伸びたレールの上を移動するロボットの拘束は(A.1)式のように表される.例えは,(A.1)式はレールの中心線である曲線の方程式をxとyで表したものである.このとき時刻tは含まれない.
移動ロボットの運動,転がり接触などの速度で表される幾何学的拘束の運動量保存則の拘束は
平面上に伸びたレールの上を移動するロボットの拘束は(A.1)式のように表される.例えは,(A.1)式はレールの中心線である曲線の方程式をxとyで表したものである.このとき時刻tは含まれない.
移動ロボットの運動,転がり接触などの速度で表される幾何学的拘束の運動量保存則の拘束は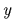 と
と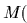 だけを含み
だけを含み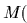 について線形な次の微分方程式で表される.
について線形な次の微分方程式で表される.
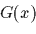 |
(91) |
ここで(A.3)式は独立な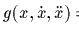 個の拘束を表し,
個の拘束を表し,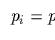 は行フルランクであると仮定する.
は行フルランクであると仮定する.
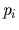 の非ホロノミックな拘束をもつ移動ロボットシステムがある.アクチェータをもたず自由に受動的に回転する車輪を持つ移動ロボットの拘束条件はこのようになる.具体的には,この式は移動ロポットの運動方程式から駆動軸トルクが零になる軸に対応する部分を選び出したものである.この場合,全軸数が一般化座標の数であり,駆動軸の数が自由度となる.
の非ホロノミックな拘束をもつ移動ロボットシステムがある.アクチェータをもたず自由に受動的に回転する車輪を持つ移動ロボットの拘束条件はこのようになる.具体的には,この式は移動ロポットの運動方程式から駆動軸トルクが零になる軸に対応する部分を選び出したものである.この場合,全軸数が一般化座標の数であり,駆動軸の数が自由度となる.
Shoichiro FUJISAWA
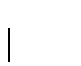 ,時間を
,時間を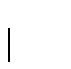 平面上に伸びたレールの上を移動するロボットの拘束は(A.1)式のように表される.例えは,(A.1)式はレールの中心線である曲線の方程式をxとyで表したものである.このとき時刻tは含まれない.
移動ロボットの運動,転がり接触などの速度で表される幾何学的拘束の運動量保存則の拘束は
平面上に伸びたレールの上を移動するロボットの拘束は(A.1)式のように表される.例えは,(A.1)式はレールの中心線である曲線の方程式をxとyで表したものである.このとき時刻tは含まれない.
移動ロボットの運動,転がり接触などの速度で表される幾何学的拘束の運動量保存則の拘束は