


Next: Mecanum Whell 方式 3輪の場合
Up: 車輪に注目した Jacobian 行列
Previous: 車輪に注目した Jacobian 行列
Contents
座標系Aにおける一致座標 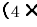 を座標Bでの点
を座標Bでの点  の座標に変換する同次
の座標に変換する同次 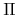 変換行列を,
変換行列を,
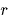 |
(43) |
と表わす.
ここで,行列は大きい太字(例えば 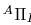 )で表す.例えば,
)で表す.例えば, 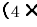 は座標系Aのベクトル
は座標系Aのベクトル 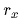 を表す.添え字はベクトルや行列の座標や要素を表す.例えば,変換行列
を表す.添え字はベクトルや行列の座標や要素を表す.例えば,変換行列 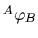 は座標系Aに対して座標系Bの位置と方向を規定する.そして
は座標系Aに対して座標系Bの位置と方向を規定する.そして 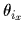 はベクトル
はベクトル 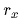 の
の 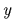 成分である.
成分である.
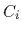 :A座標系のx軸とB座標系(反時計方向で)の間A座標系のZ軸まわりの回転変位量.
:A座標系のx軸とB座標系(反時計方向で)の間A座標系のZ軸まわりの回転変位量.
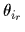 :車輪の軸中心まわりの
:車輪の軸中心まわりの 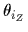 のx軸に平行な車輪i(i=1,2,3,4に対して)の回転の変位量.
のx軸に平行な車輪i(i=1,2,3,4に対して)の回転の変位量.
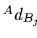 :ローラの軸と並ぶ軸まわりの床と接触した車輪i(i=1,2,3,4に対して)の回転の変位量.
:ローラの軸と並ぶ軸まわりの床と接触した車輪i(i=1,2,3,4に対して)の回転の変位量.
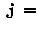 :車輪の軸中心まわりの
:車輪の軸中心まわりの 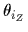 のz軸に平行な車輪i(i=1,2,3,4に対して)の回転の変位量.
のz軸に平行な車輪i(i=1,2,3,4に対して)の回転の変位量.
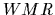 :AとB座標系の原点の間のA座標系のj軸(
:AとB座標系の原点の間のA座標系のj軸( ![$ j=[x,y,z] $](img161.gif) に対して)に沿った変換量.
この
に対して)に沿った変換量.
この 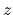 モデルのある2つのAとBの座標系が零でない
モデルのある2つのAとBの座標系が零でない 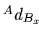 と
と 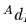 座標がお互いに関係するとして位置付けられるので,それぞれの変換行列は変換
座標がお互いに関係するとして位置付けられるので,それぞれの変換行列は変換  と
と 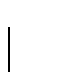 と
と 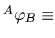 を含まなければならない.我々は座標系がz軸まわりの関係ですべての回転を走行の表面とz軸が直交するすべての座標系を設定する.すなわち,変換行列
を含まなければならない.我々は座標系がz軸まわりの関係ですべての回転を走行の表面とz軸が直交するすべての座標系を設定する.すなわち,変換行列 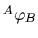 は座標系Aのz軸まわりの回転変位量
は座標系Aのz軸まわりの回転変位量
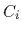 を包含する.そして変換
を包含する.そして変換 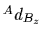 と
と  と
と 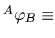 はそれぞれ座標軸に沿う.
はそれぞれ座標軸に沿う.
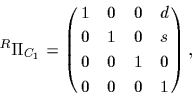 |
(44) |
座標変換行列を車輪 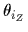 に対して表すと,
に対して表すと,
 :
:
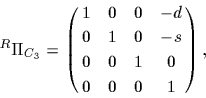 |
(45) |
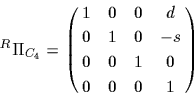 |
(46) |
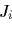 |
(47) |
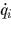 |
(48) |
となる.
各車輪iに対するJacobian 行列 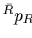 は,車輪速度
は,車輪速度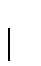 の線形結合としてのロボット速度
の線形結合としてのロボット速度
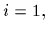 で,
で,
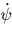 |
(49) |
と表せる.(ここで,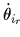 )
ロボット速度ベクトル
)
ロボット速度ベクトル
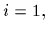 は,移動ロボット速度
は,移動ロボット速度 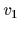 と
と 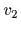 ,そして回転ロボット速度
,そして回転ロボット速度 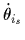 の3成分からなる.全方向移動車輪iの3自由度は,車輪ハブ回転,ローラ回転そして点接触回りの回転の車輪速度ベクトル
の3成分からなる.全方向移動車輪iの3自由度は,車輪ハブ回転,ローラ回転そして点接触回りの回転の車輪速度ベクトル 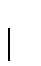 の3成分からなる:
の3成分からなる:
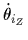 と
と
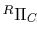 と
と
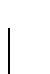 がそれぞれ一致する.全方向車輪Jacobian 行列
がそれぞれ一致する.全方向車輪Jacobian 行列 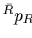 は変換行列
は変換行列
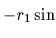 から構成される.車輪とローラの半径はrとs,ローラの角度は
から構成される.車輪とローラの半径はrとs,ローラの角度は 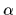 とする.
とする.
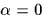 |
(50) |
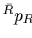 の決定は(
の決定は(
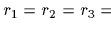 )であるので,(4)式の全方向車輪ヤコビ行列は
)であるので,(4)式の全方向車輪ヤコビ行列は 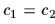 か180°でない時は一つでない.;例えば,ローラと車輪方向が並んでいない時.ローラの角度が±45°なので,それぞれの車輪ヤコビ行列のランクは3である,それぞれの車輪のは3自由度を示す.
簡単な構成のために,すべての車輪は等しいとする.したがって,すべての車輪とローラの半径は等しい(例えば,
か180°でない時は一つでない.;例えば,ローラと車輪方向が並んでいない時.ローラの角度が±45°なので,それぞれの車輪ヤコビ行列のランクは3である,それぞれの車輪のは3自由度を示す.
簡単な構成のために,すべての車輪は等しいとする.したがって,すべての車輪とローラの半径は等しい(例えば,
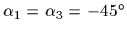 と
と
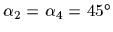 ).すべて4つの車輪のローラの角度の大きさは同様に等しい.車輪1と2は車輪2と4のローラ角度の逆になるように装着されている.(すなわち,
).すべて4つの車輪のローラの角度の大きさは同様に等しい.車輪1と2は車輪2と4のローラ角度の逆になるように装着されている.(すなわち,
 と
と
 ).この全方向車輪に対するJacobian 行列から,それぞれの車輪に対する運動の式を導く:
車輪1の場合:
).この全方向車輪に対するJacobian 行列から,それぞれの車輪に対する運動の式を導く:
車輪1の場合:
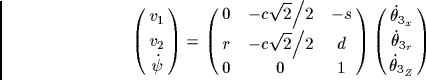 |
(51) |
車輪2の場合:
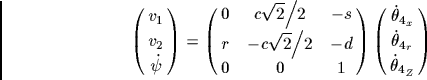 |
(52) |
車輪3の場合:
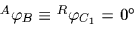 |
(53) |
車輪4の場合:
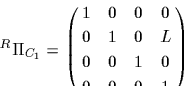 |
(54) |



Next: Mecanum Whell 方式 3輪の場合
Up: 車輪に注目した Jacobian 行列
Previous: 車輪に注目した Jacobian 行列
Contents
Shoichiro FUJISAWA
 と
と 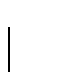 と
と  :
:
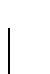 がそれぞれ一致する.全方向車輪Jacobian 行列
がそれぞれ一致する.全方向車輪Jacobian 行列  ).この全方向車輪に対するJacobian 行列から,それぞれの車輪に対する運動の式を導く:
車輪1の場合:
).この全方向車輪に対するJacobian 行列から,それぞれの車輪に対する運動の式を導く:
車輪1の場合: