


: アフィン空間 の構造
: 微分と微分
: 微分と微分
目次
よく知られるように実数関数
の 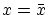 での
での
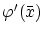 は
は
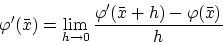 |
(1.1) |
で定義されています。
しかし,この定義を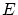 のような関数集合に適用することはできません。
分母の
のような関数集合に適用することはできません。
分母の
は定義できますが,これを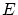 の元
の元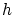 で割る演算できないからです。
で割る演算できないからです。
割り算を使わない工夫が必要になります。そこで上記の微分の定義式(![[*]](/icons.gif/cross_ref_motif.gif) )を次のように
書き換えてみます。
)を次のように
書き換えてみます。
ただし,
とします。
ここで,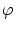 が微分可能であれば,上の微分の定義式(
が微分可能であれば,上の微分の定義式(![[*]](/icons.gif/cross_ref_motif.gif) )
の右辺の極限が
左辺と一致するのですから,
)
の右辺の極限が
左辺と一致するのですから,
が成立っている。
そこで,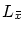 が任意の
が任意の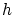 について
について
| |
|
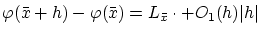 |
(1.3) |
| |
|
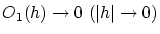 |
(1.4) |
を充たすとき,この 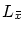 を
を 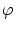 の
の 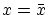 での微分
と定義すことにします。
での微分
と定義すことにします。
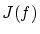 についても,見かけの形式は
についても,見かけの形式は
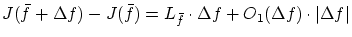 |
|
|
(1.5) |
とするべきでしょう。
このとき,和
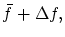 積
積
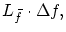 ノルム
ノルム 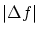 はどのような意味を持つか考察しましょう。
はどのような意味を持つか考察しましょう。



: アフィン空間 の構造
: 微分と微分
: 微分と微分
目次
Yasunari SHIDAMA
![]() )を次のように
書き換えてみます。
)を次のように
書き換えてみます。
![]() が任意の
が任意の![]() について
について
![]() を
を ![]() の
の ![]() での微分
と定義すことにします。
での微分
と定義すことにします。
![]() についても,見かけの形式は
についても,見かけの形式は
![]() 積
積
![]() ノルム
ノルム ![]() はどのような意味を持つか考察しましょう。
はどのような意味を持つか考察しましょう。