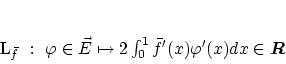


: の線形性と連続性
: 微分と微分
: 微分の再定義
目次
ここで
という空間を考えます。
に対して,
よって
また
さらに,
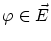 に対して
に対して
とすると 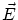 は前章で扱ったノルム空間です。
は前章で扱ったノルム空間です。
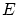 に付随した
に付随した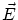 を導入した理由は,次によります。
を導入した理由は,次によります。
はバナハ空間![$C^1[0,1]$](img15.gif) の部分集合ではありますが,これの任意の
元
の部分集合ではありますが,これの任意の
元
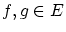 については
については
となって
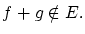 また
また
であるので
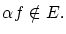 です。つまり
です。つまり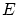 は線形空間の構造は持っていません。
は線形空間の構造は持っていません。
ただし
よって
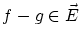 です。
です。
また,
とすると
です。
ここで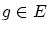 とすると
とすると
より
「線形空間もどき」の性質があるわけです。
この空間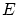 を(線形空間
を(線形空間 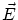 をともなう) アフィン空間とよびます。
をともなう) アフィン空間とよびます。
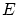 自身は線形空間ではないが,
自身は線形空間ではないが,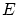 の元
の元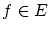 を一つ固定して原点のように
扱えば,
を一つ固定して原点のように
扱えば,
は線形空間になっています。また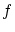 に変動として
に変動として
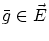 を加えた
を加えた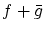 も
も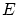 の元になっています。
の元になっています。
以上によって変分法の第1章の議論を再び持ち出すことが可能になりました。
すなわち,まず
とおきます。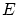 上の写像
上の写像
について,
であり,第1章の計算を繰り返して
を得ます。
さてここで,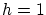 とすると
とすると
このとき(1.5)式の
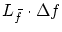 は
は
で定義するべきでしょう。
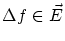 の任意性を考えれば,上の式は
の任意性を考えれば,上の式は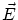 から
から
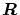 への写像
への写像
を定義しているものと考えらます。



: の線形性と連続性
: 微分と微分
: 微分の再定義
目次
Yasunari SHIDAMA
![]() に付随した
に付随した![]() を導入した理由は,次によります。
を導入した理由は,次によります。
![]() とすると
とすると
![]() を(線形空間
を(線形空間 ![]() をともなう) アフィン空間とよびます。
をともなう) アフィン空間とよびます。
![]() 自身は線形空間ではないが,
自身は線形空間ではないが,![]() の元
の元![]() を一つ固定して原点のように
扱えば,
を一つ固定して原点のように
扱えば,
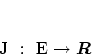
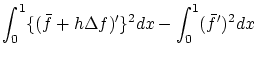
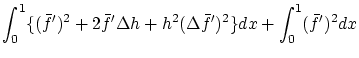
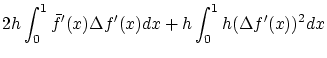
![]() とすると
とすると