


: 微分の再定義
: 微分
: 微分
目次
大分道草を食べましたが,再び最初に扱った変分問題に戻りましょう。
それは汎関数
を条件
で最小化するものでした。
この問題について,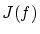 を関数の集合
を関数の集合
から
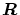 への写像
への写像
について何らかの意味の微分の概念を導入し
実数値関数の極小条件
のような扱いはできないだろうかという動機で,前章までに,
まず定義域である関数の集合についての数学的構造を調べました。
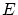 をその部分集合として含む
をその部分集合として含む![$C^1[0,1]$](img15.gif) などは関数空間と呼ばれ,特に
Banach空間というものになっていました。
などは関数空間と呼ばれ,特に
Banach空間というものになっていました。
これには,要素
![$f,g \in C^1[0,1]$](img16.gif) の加算
の加算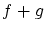 と,係数体の元
と,係数体の元
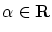 によるスカラー倍
によるスカラー倍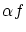 という代数的な構造(線形空間の構造)が定義され,
という代数的な構造(線形空間の構造)が定義され,
要素
![$f \in C^1[0,1]$](img20.gif) にはノルム
にはノルム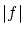 も定義され,
さらに実数の集合のような収束の扱いも可能でした。
も定義され,
さらに実数の集合のような収束の扱いも可能でした。
ここでは本題の,これら関数空間上での微分の概念を扱うことにします。
そのためには
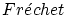 微分という概念が必要になってきます。
また,集合
微分という概念が必要になってきます。
また,集合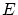 だけではなくそれに付随した
だけではなくそれに付随した
も用いることになります。

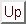


: 微分の再定義
: 微分
: 微分
目次
Yasunari SHIDAMA
![]() を関数の集合
を関数の集合
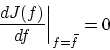
![]() 微分という概念が必要になってきます。
また,集合
微分という概念が必要になってきます。
また,集合![]() だけではなくそれに付随した
だけではなくそれに付随した