

Next: 一般的な最適制御
Up: 最適制御理論
Previous: 概要
ラグランジュの未定乗数法によると
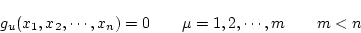 |
(2.172) |
という拘束条件のもとで、連続関数
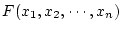 を極値にするには
を極値にするには
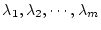 を未定の乗数としたとき、次の補助関数
を未定の乗数としたとき、次の補助関数
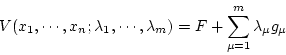 |
(2.173) |
の、
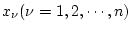 および
および 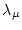 に対する
極値を求めればよい。
に対する
極値を求めればよい。
制御系の場合はシステム方程式
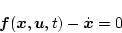 |
(2.174) |
が拘束条件となり、評価関数
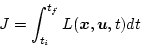 |
(2.175) |
を最小とする問題となるから、補助関数は
となり、この
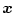 および
および
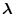 に対する極小値を求めれば、
最適制御が得られる。
に対する極小値を求めれば、
最適制御が得られる。
いま、ある軌道を通ったとき
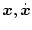 であり、その近傍を通ったとき
であり、その近傍を通ったとき
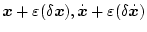 (
(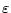 は微少な定数)
であったとする。そのとき両者の補助関数の差を
は微少な定数)
であったとする。そのとき両者の補助関数の差を 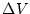 とすると
とすると
![\begin{displaymath}
\Delta V = \int^{t_f}_{t_i} [L' \{ (\mbox{\boldmath$x$} + \v...
... L' \{ \mbox{\boldmath$x$},\dot{\mbox{\boldmath$x$}},t \} ]d t
\end{displaymath}](img435.png) |
(2.177) |
になる。上式の被積分関数は Taylor 展開をすると
となる。したがって
![\begin{displaymath}
\Delta V(\varepsilon) = \int^{t_f}_{t_i} \left[
\varepsilon...
...$x$}}
+ (\varepsilon^2,\varepsilon^3,\cdots, の項) \right]d t
\end{displaymath}](img440.png) |
(2.179) |
になる。補助関数が極値となるための必要条件は
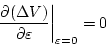 |
(2.180) |
である。これから
![\begin{displaymath}
\int^{t_f}_{t_i} \left[
\frac{\partial L'}{\partial \mbox{\...
...oldmath$x$}}}
\delta \dot{\mbox{\boldmath$x$}} \right]d t = 0
\end{displaymath}](img442.png) |
(2.181) |
という条件が得られる。
この積分の第2項を部分積分すると、
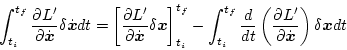 |
(2.182) |
となる。最終状態指定の場合は
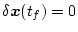 であり、初期状態も
であり、初期状態も
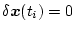 ゆえ、上式右辺第一項は0となり、したがって
(2.181)式は
ゆえ、上式右辺第一項は0となり、したがって
(2.181)式は
![\begin{displaymath}
\int^{t_f}_{t_i} \left[
\frac{\partial L'}{\partial \dot{\m...
...math$x$}}} \right)
\right] \delta \mbox{\boldmath$x$} d t = 0
\end{displaymath}](img446.png) |
(2.183) |
になる。すべての
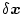 に対してこの式が成立するためには
に対してこの式が成立するためには
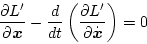 |
(2.184) |
が条件となる。これをオイラー(Euler)方程式という。この式に(2.176)式
を適用すると
いま
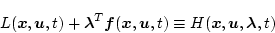 |
(2.186) |
とする。これをハミルトン関数(またはH関数)という。そのとき
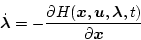 |
(2.187) |
になる。
同様にして、
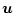 に対するオイラー方程式は
に対するオイラー方程式は
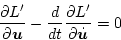 |
(2.188) |
となり、
となる。
であるので、以上をまとめると
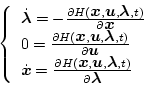 |
(2.191) |
となる。
最適制御を求める手順
(第1段階)
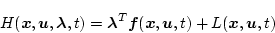 |
(2.192) |
を求める。
(第2段階)
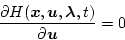 |
(2.193) |
より
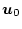 を求める。
を求める。
(第3段階)
最適の 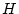 関数
関数
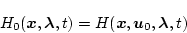 |
(2.194) |
を求める。
(第4段階)
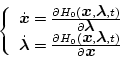 |
(2.195) |
を
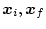 の境界条件で
の境界条件で 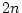 組の方程式を解く。
組の方程式を解く。
(第5段階)
上記で求めた結果を
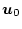 に代入して最適制御を得る。なお最終時刻
に代入して最適制御を得る。なお最終時刻 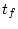 が
規定されていないときは
が
規定されていないときは
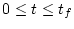 の期間中
の期間中
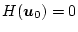 となる。
となる。
[例1]
図 2.16:
![\begin{figure}\begin{center}
\psbox[scale=0.80]{eps/2-7-2.eps}\\
\end{center} \end{figure}](img474.png) |
図2.16の一次遅れ制御対象に対し、最小の制御力 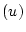 によって制御量
によって制御量 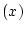 の
自乗積分値を最小にする最適制御を求める。
の
自乗積分値を最小にする最適制御を求める。
評価関数は
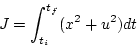 |
(2.196) |
システム方程式は
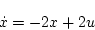 |
(2.197) |
(第1段階)
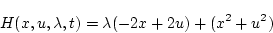 |
(2.198) |
(第2段階)
| |
|
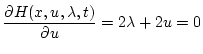 |
(2.199) |
| |
|
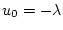 |
|
(第3段階)
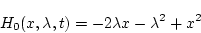 |
(2.200) |
(第4段階)
| |
|
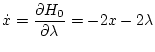 |
(2.201) |
| |
|
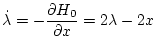 |
(2.202) |
両式より
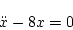 |
(2.203) |
解は
| |
|
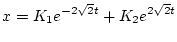 |
(2.204) |
| |
|
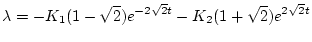 |
(2.205) |
境界条件として、
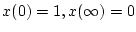 を代入すると、
を代入すると、
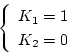 |
(2.206) |
ゆえに
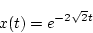 |
(2.207) |
(第5段階)
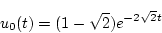 |
(2.208) |
[例2]
前例で
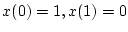 とした場合、(第4段階)で
とした場合、(第4段階)で
| |
|
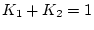 |
(2.209) |
| |
|
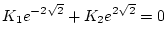 |
(2.210) |
となり
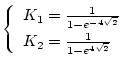 |
|
|
(2.211) |
(第5段階)
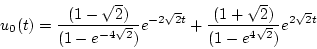 |
(2.212) |
この場合は 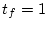 と指定されているので
と指定されているので
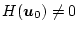 である。
である。
[例3]
上記の制御対象に対し、最小制御力で制御量の自乗積分偏差も最小、かつ最短時間で
目標に達せしめる最適制御を求める。
評価関数は
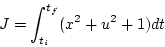 |
(2.213) |
システム方程式は
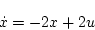 |
(2.214) |
であり、 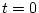 で
で
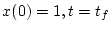 で
で 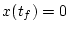 とする。
とする。
(第1段階)
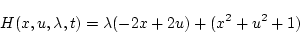 |
(2.215) |
(第2段階)
| |
|
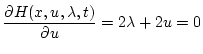 |
(2.216) |
| |
|
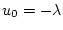 |
(2.217) |
(第3段階)
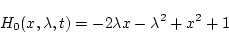 |
(2.218) |
(第4段階)
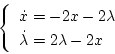 |
(2.219) |
解は
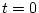 で
で 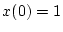 ゆえ
ゆえ
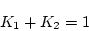 |
(2.223) |
である。また 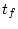 が指定されていないので、
が指定されていないので、
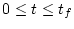 で
で
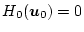 である。したがって
である。したがって 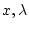 を
を 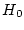 に代入すると
に代入すると
したがって
となる。 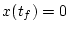 となるためには
となるためには 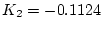 でなければならないから、
でなければならないから、
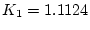 となる。
となる。
(第5段階)
[例4]
図 2.17:
![\begin{figure}\begin{center}
\psbox[scale=0.80]{eps/2-7-3.eps} \end{center} \end{figure}](img535.png) |
図2.17の系において最短時間で目標に達するための最適制御を求める。
システム方程式
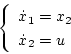 |
(2.227) |
評価関数
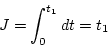 |
(2.228) |
(第1段階)
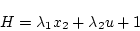 |
(2.229) |
(第2段階)
この式の極大を得るには、
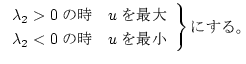 このことは、オンオフ制御(バング・バング制御)を意味する。オンとオフの
切換条件は
このことは、オンオフ制御(バング・バング制御)を意味する。オンとオフの
切換条件は 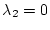 のところとなる。しかし実際にこの方法で
のところとなる。しかし実際にこの方法で
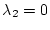 のところを見出すのは容易ではない。この問題は後述するような非線形制御系の
問題として別の方法で容易に得ることができる。
のところを見出すのは容易ではない。この問題は後述するような非線形制御系の
問題として別の方法で容易に得ることができる。


Next: 一般的な最適制御
Up: 最適制御理論
Previous: 概要
Yasunari SHIDAMA
平成15年5月12日
![]() であり、その近傍を通ったとき
であり、その近傍を通ったとき
![]() (
(![]() は微少な定数)
であったとする。そのとき両者の補助関数の差を
は微少な定数)
であったとする。そのとき両者の補助関数の差を ![]() とすると
とすると
![]() に対するオイラー方程式は
に対するオイラー方程式は
![]() に代入して最適制御を得る。なお最終時刻
に代入して最適制御を得る。なお最終時刻 ![]() が
規定されていないときは
が
規定されていないときは
![]() の期間中
の期間中
![]() となる。
となる。
![]() によって制御量
によって制御量 ![]() の
自乗積分値を最小にする最適制御を求める。
の
自乗積分値を最小にする最適制御を求める。
![]() とした場合、(第4段階)で
とした場合、(第4段階)で
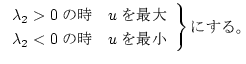 このことは、オンオフ制御(バング・バング制御)を意味する。オンとオフの
切換条件は
このことは、オンオフ制御(バング・バング制御)を意味する。オンとオフの
切換条件は ![]() のところとなる。しかし実際にこの方法で
のところとなる。しかし実際にこの方法で
![]() のところを見出すのは容易ではない。この問題は後述するような非線形制御系の
問題として別の方法で容易に得ることができる。
のところを見出すのは容易ではない。この問題は後述するような非線形制御系の
問題として別の方法で容易に得ることができる。