Next: サーボ問題
Up: 追値制御系の最適制御
Previous: 概要
システム方程式を
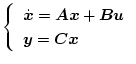 |
|
|
(2.415) |
とした場合、レギュレータ問題では評価関数は通常
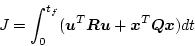 |
(2.416) |
で与えられるが、トラッキング問題では目標入力を
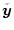 で表示すると、
追随性を良くするため
で表示すると、
追随性を良くするため
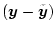 を含む評価関数として
を含む評価関数として
![\begin{displaymath}
J=\int_0^{t_f}[\mbox{\boldmath$u$}^T \mbox{\boldmath$R$}\mbo...
...ldmath$Q$}(\mbox{\boldmath$y$}-\tilde{\mbox{\boldmath$y$}})]dt
\end{displaymath}](img865.png) |
(2.417) |
のようにすればよい。
しかしシステムによっては出力の変化が急激でないことが望ましい場合もある。
その時は評価関数として
![\begin{displaymath}
J=\int_0^{t_f}[\mbox{\boldmath$u$}^T \mbox{\boldmath$R$}\mbo...
...math$Q$}_2(\mbox{\boldmath$y$}-\tilde{\mbox{\boldmath$y$}})]dt
\end{displaymath}](img866.png) |
(2.418) |
のように、
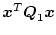 の項を含めることが考えられる。
ところがこの項は
の項を含めることが考えられる。
ところがこの項は
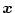 をできるだけ小さくしようと作用し、
をできるだけ小さくしようと作用し、
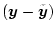 は
は
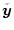 に近づけるために
に近づけるために
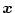 を大きくしようと作用するので両者が相反する。そこでいま
を大きくしようと作用するので両者が相反する。そこでいま
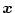 を
を
| |
|
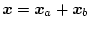 |
(2.419) |
| |
|
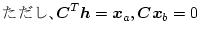 |
|
というように、
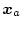 と
と
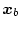 を直交する成分に分ける。
を直交する成分に分ける。
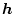 はあるベクトルである。こうすると
はあるベクトルである。こうすると
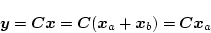 |
(2.420) |
となり、
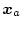 は
は
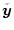 に従う成分、
に従う成分、
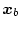 は基準線近傍
の変動する成分として考えられる。したがって上記評価関数中の
は基準線近傍
の変動する成分として考えられる。したがって上記評価関数中の
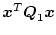 の代わりに、
の代わりに、
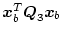 を入れると
を入れると
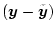 とは反しなくなる。(2.426)式より
とは反しなくなる。(2.426)式より
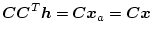 |
|
|
(2.421) |
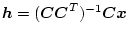 |
|
|
(2.422) |
になるので、
![\begin{displaymath}
\mbox{\boldmath$x$}_b=\mbox{\boldmath$x$}-\mbox{\boldmath$x$...
...x{\boldmath$C$}^T)^{-1}\mbox{\boldmath$C$}]\mbox{\boldmath$x$}
\end{displaymath}](img877.png) |
(2.423) |
となる。そこで
![\begin{displaymath}
\mbox{\boldmath$Q$}_1=[\mbox{\boldmath$I$}-\mbox{\boldmath$C...
...x{\boldmath$C$}\mbox{\boldmath$C$}^T)^{-1}\mbox{\boldmath$C$}]
\end{displaymath}](img878.png) |
(2.424) |
とおけば
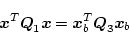 |
(2.425) |
となり、これが応答を滑らか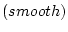 にする評価を分担する。
にする評価を分担する。
[例]
である。このとき
になることが分る。
いまここで
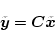 |
(2.431) |
なる
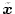 を規定すると、この
を規定すると、この
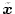 は目標値
は目標値
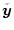 なる出力を出すための状態変数であることを意味する。この
なる出力を出すための状態変数であることを意味する。この
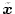 は
は
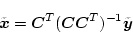 |
(2.432) |
で表される。
ここで
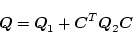 |
(2.433) |
としたとき
となるが(2.431)式,(2.438)式,(2.439)式より
同様にして
となるので、(2.441)式は
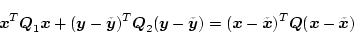 |
(2.437) |
となる。したがって(2.425)式の評価関数は
![\begin{displaymath}
J=\int_0^{t_f}[\mbox{\boldmath$u$}^T \mbox{\boldmath$R$}\mbo...
...dmath$Q$}
(\mbox{\boldmath$x$}-\tilde{\mbox{\boldmath$x$}})]dt
\end{displaymath}](img903.png) |
(2.438) |
で表示をすれば、滑らかさを考慮したものとなる。この場合(2.440)
式で表される
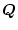 のうち
のうち
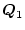 が滑らかさを、
が滑らかさを、
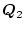 が目標への追随性
を良くするための重み係数となる。
が目標への追随性
を良くするための重み係数となる。



Next: サーボ問題
Up: 追値制御系の最適制御
Previous: 概要
Yasunari SHIDAMA
平成15年5月12日