


Next: 拡張型パーフェクト・モデル・フォローイング
Up: 追値制御系の最適制御
Previous: パーフェクト・モデル・フォローイング
前記のパーフェクト・モデル・フォロイング系ではモデルを実際に構成し、
その出力をプラントの入力に使用する。これを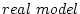 ということがある。
これに対してモデルを実際には構成せずに
プラントのフィードバックによってモデルと同じ特性をもたせる系を
モデル・マッチングという。
またこのようなモデルを
ということがある。
これに対してモデルを実際には構成せずに
プラントのフィードバックによってモデルと同じ特性をもたせる系を
モデル・マッチングという。
またこのようなモデルを
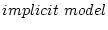 ということがある。
ということがある。
前項の(2.472)式において
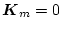 とすると
とすると
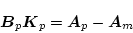 |
(2.480) |
になるので、
![\begin{displaymath}
rank\mbox{\boldmath$B$}_{p}=rank[\mbox{\boldmath$B$}_{p},(\mbox{\boldmath$A$}_{p}-\mbox{\boldmath$A$}_{m})]
\end{displaymath}](img982.png) |
(2.481) |
であれば
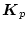 が求められる。(2.474)式は
が求められる。(2.474)式は
となるから、
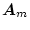 が安定となるように選定してあれば、
が安定となるように選定してあれば、
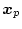 は
は
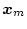 と同じ応答をする。すなわち(2.490),(2.473)
式より求めた
と同じ応答をする。すなわち(2.490),(2.473)
式より求めた
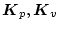 を用いて制御系を構成すれば
プラントにモデルと同じ特性を持たせることができる。
を用いて制御系を構成すれば
プラントにモデルと同じ特性を持たせることができる。
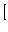 例
例![$]$](img114.png) プラントの状態方程式を
プラントの状態方程式を
![\begin{displaymath}
\dot{\mbox{\boldmath$x$}}_{p}=
\left[
\begin{array}{cc}
0&1\...
...in{array}{c}
0\\
1
\end{array}\right]
\mbox{\boldmath$u$}_{p}
\end{displaymath}](img1013.png) |
(2.482) |
モデルの状態方程式を
![\begin{displaymath}
\dot{\mbox{\boldmath$x$}}_{m}=
\left[
\begin{array}{cc}
0&1\...
...in{array}{c}
0\\
2
\end{array}\right]
\mbox{\boldmath$u$}_{m}
\end{displaymath}](img1014.png) |
(2.483) |
とする。このとき
![\begin{displaymath}
\mbox{\boldmath$B$}_{p}\mbox{\boldmath$K$}_{p}=\mbox{\boldma...
...ight]
=
\left[
\begin{array}{cc}
0&0\\
4&3
\end{array}\right]
\end{displaymath}](img1015.png) |
(2.484) |
より
![\begin{displaymath}
\mbox{\boldmath$K$}_{p}=
\left[
\begin{array}{cc}
4&3
\end{array}\right]
\end{displaymath}](img1016.png) |
(2.485) |
になり
![\begin{displaymath}
\mbox{\boldmath$B$}_{p}\mbox{\boldmath$K$}_{v}=\mbox{\boldmath$B$}_{m}=
\left[
\begin{array}{c}
0\\
2
\end{array}\right]
\end{displaymath}](img1017.png) |
(2.486) |
より
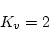 |
(2.487) |
となる。このときプラントの入出力関係は
となってモデルのそれと等しくなる。
ブロック図は図2.27のごとくなる。
図 2.27:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/2-9-5.eps} \end{center} \end{figure}](img1021.png) |



Next: 拡張型パーフェクト・モデル・フォローイング
Up: 追値制御系の最適制御
Previous: パーフェクト・モデル・フォローイング
Yasunari SHIDAMA
平成15年5月12日
![]() ということがある。
これに対してモデルを実際には構成せずに
プラントのフィードバックによってモデルと同じ特性をもたせる系を
モデル・マッチングという。
またこのようなモデルを
ということがある。
これに対してモデルを実際には構成せずに
プラントのフィードバックによってモデルと同じ特性をもたせる系を
モデル・マッチングという。
またこのようなモデルを
![]() ということがある。
ということがある。
![]() とすると
とすると