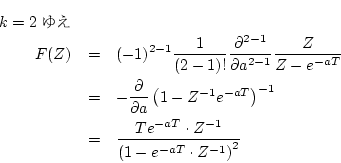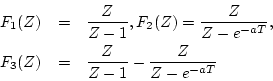

Next: 逆変換
Up: サンプル値の表現と変換
Previous: サンプル値の表現
(3.4)式において
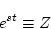 |
(3.11) |
とおくと
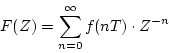 |
(3.12) |
となり、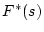 は
は の関数となる。このように
の関数となる。このように の関数に変換することを
の関数に変換することを
 変換(
変換( -transform)という。
-transform)という。
与えられた関数が時間領域で表示されている場合には、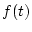 の
の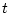 を
を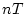 に
書き換え
に
書き換え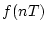 とし、(3.12)式に適用する。
とし、(3.12)式に適用する。
なお、この場合
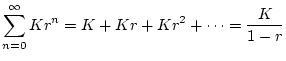 |
|
|
(3.13) |
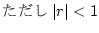 |
|
|
|
の公式を用いて簡単化する。
[例]
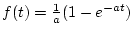 の場合
の場合
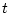 を
を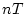 に置き換え
に置き換え
とし、(3.12)式に適用すると
となる。
(3.8)式より
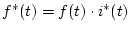 ゆえこれをラプラス変換すると、
ゆえこれをラプラス変換すると、
で表される。
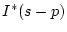 は単位パルス列信号ゆえ、(3.4)式より
は単位パルス列信号ゆえ、(3.4)式より
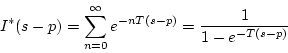 |
(3.15) |
となるので
となる。
ただし、
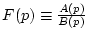
で分母の次数の方が高いとする。
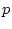 を
を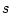 に書き換え
に書き換え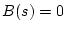 の根を
の根を
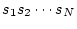 とし、重根を
含まないとき
とし、重根を
含まないとき
となる。
多重根の場合、例えば
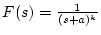 の場合
の場合
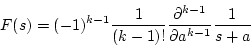 |
(3.18) |
で表されるから
となる。したがって、与えられた関数が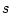 領域で
表示されている場合の
領域で
表示されている場合の 変換の
手順は次のごとくである。
変換の
手順は次のごとくである。
重根を含まない場合
- #1.
-
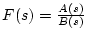 とする。
とする。
- #2.
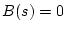 の根
の根
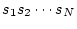 を求める。
を求める。
- #3.
-
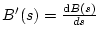 を求める。
を求める。
- #4.
-
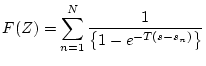 より
より 変換を行う。
変換を行う。
ただし、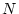 は
は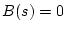 の根の数
の根の数
重根を含む場合、重根の部分を
として、 変換を行う。
変換を行う。
[例1]
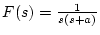 の
の 変換を求める。
変換を求める。
- #1.
-
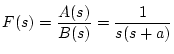
- #2.
-
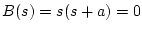
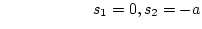
- #3.
-
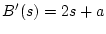
- #4.
-
![$\begin{array}[t]{rcl}
F(Z)
& = & \displaystyle \sum_{n=1}^{N} \frac{1}{2s_{n}+...
... \frac{1}{a}
\left\{ \frac{Z}{Z-1}-
\frac{Z}
{Z-e^{-aT}}\right\}
\end{array}$](img101.png)
[例2]
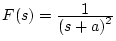 の
の 変換を求める。
変換を求める。
代表的な関数の 変換表を表3.1に示す。
変換表を表3.1に示す。
表 3.1:
 変換表
変換表
| |
F(s) |
f(nT) |
F(Z) |
| 1 |
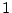 |
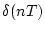 |
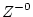 |
| 2 |
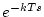 |
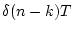 |
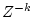 |
| 3 |
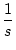 |
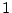 |
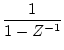 |
| 4 |
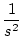 |
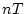 |
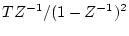 |
| 5 |
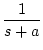 |
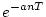 |
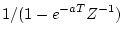 |
| 6 |
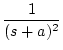 |
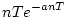 |
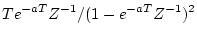 |
| 7 |
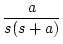 |
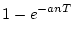 |
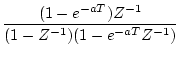 |
| 8 |
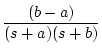 |
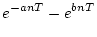 |
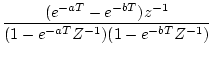 |
| 9 |
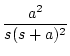 |
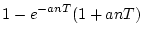 |
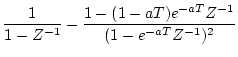 |
| 10 |
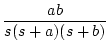 |
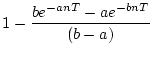 |
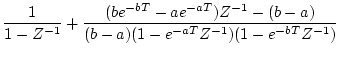 |
なお
のとき
である。(すなわち、先に 変換をして積を求めてはならない)
変換をして積を求めてはならない)
例えば
のとき、表3.1より
であり、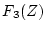 は
は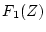 と
と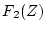 の積とは異なる。
の積とは異なる。

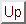

Next: 逆変換
Up: サンプル値の表現と変換
Previous: サンプル値の表現
Yasunari SHIDAMA
平成15年6月9日
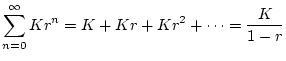
![]() の場合
の場合
![]() を
を![]() に置き換え
に置き換え
![]() は単位パルス列信号ゆえ、(3.4)式より
は単位パルス列信号ゆえ、(3.4)式より
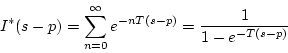
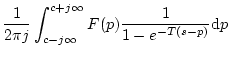
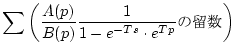
![]() を
を![]() に書き換え
に書き換え![]() の根を
の根を
![]() とし、重根を
含まないとき
とし、重根を
含まないとき
![$\displaystyle \sum_{n=1}^{N}\frac{A(s_{n})}{B'(s_{n})}
\frac{1}{1-e^{-T(s-s_{n})}}\equiv Z\left[F(s)\right]$](img84.png)
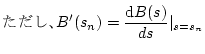
![]() の場合
の場合
![$\displaystyle (-1)^{k-1}\frac{1}{(k-1)!}
\frac{\partial^{k-1}}
{\partial a^{k-1}}
Z\left[\frac{1}
{s+a}\right]$](img89.png)
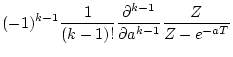
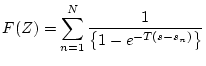 より
より![]() の
の![]() 変換を求める。
変換を求める。
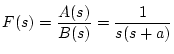
![$\begin{array}[t]{rcl}
F(Z)
& = & \displaystyle \sum_{n=1}^{N} \frac{1}{2s_{n}+...
... \frac{1}{a}
\left\{ \frac{Z}{Z-1}-
\frac{Z}
{Z-e^{-aT}}\right\}
\end{array}$](img101.png)