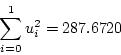

Next: 有限時間整定法
Up: 離散値系の各種制御法
Previous: レギュレータ問題
前項で述べたように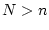 の場合は目標値に到達する以外に他の拘束を加える
ことができる。そこで任意の初期状態
の場合は目標値に到達する以外に他の拘束を加える
ことができる。そこで任意の初期状態
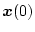 から目標値
から目標値
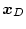 に
に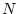 サンプリングで到達させると共に、その制御に要するエネルギを最小にする場
合を考える。
サンプリングで到達させると共に、その制御に要するエネルギを最小にする場
合を考える。
制御エネルギとしては、単入力の場合
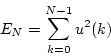 |
(4.157) |
と定義する。
もし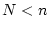 の場合は目標値には到達できない。その時は目標値と最終状態変数との差、
すなわち誤差ベクトルの測度
の場合は目標値には到達できない。その時は目標値と最終状態変数との差、
すなわち誤差ベクトルの測度
![\begin{displaymath}[\mbox{\boldmath$x$}_D-\mbox{\boldmath$x$}(N)]^T[\mbox{\boldmath$x$}_D-\mbox{\boldmath$x$}(N)]
\end{displaymath}](img368.png) |
(4.158) |
を最小にするように考える。
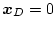 のときは
のときは
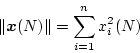 |
(4.159) |
となる。
目標値に到達する為には(4.150)式から
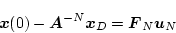 |
(4.160) |
を満足する
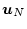 を定めればよい。特に
を定めればよい。特に
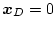 のときは
のときは
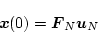 |
(4.161) |
となる。
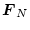 は
は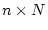 の非正方行列である。したがって
の非正方行列である。したがって
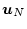 を求めるためには
非正方行列の逆行列を求めなければならない。
を求めるためには
非正方行列の逆行列を求めなければならない。
いま連立方程式
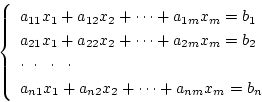 |
(4.162) |
をマトリクス表示すると
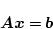 |
(4.163) |
ただし
となる。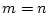 のときは
のときは
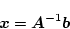 |
(4.164) |
として扱えるが、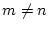 のときは
のときは
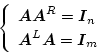 |
(4.165) |
とする。
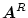 をright inverse,
をright inverse,
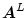 をleft inverse という。
これを用いると(4.164)式の解
をleft inverse という。
これを用いると(4.164)式の解
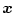 は
は
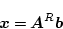 |
(4.166) |
と書ける。何故ならこの式に
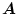 を左から掛けると
を左から掛けると
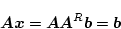 |
(4.167) |
となって (4.164)式となるからである。いま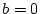 の場合、すなわち
の場合、すなわち
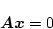 |
(4.168) |
という同次方程式を考える。この時
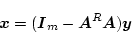 |
(4.169) |
が解となる。何故なら
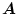 を左から掛けると
を左から掛けると
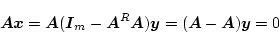 |
(4.170) |
となるからである。ここで
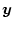 は
は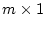 の任意のベクトルである。したがって
(4.164)式の一般解は
の任意のベクトルである。したがって
(4.164)式の一般解は
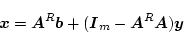 |
(4.171) |
となり、
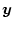 は任意ゆえ
は任意ゆえ
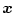 は無数に存在し、
は無数に存在し、
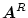 も多数存在す
る。
も多数存在す
る。
[例]
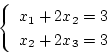 |
(4.172) |
の場合
であるが、任意の
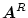 として次の場合を考える。
として次の場合を考える。
![\begin{displaymath}
\mbox{\boldmath$A$}^R = \left[ \begin{array}{cr}
1 & 2 \\
0 & -1 \\
0 & 1
\end{array} \right]
\end{displaymath}](img398.png) |
(4.173) |
これは
![\begin{displaymath}
\mbox{\boldmath$A$}\mbox{\boldmath$A$}^R = \left[ \begin{ar...
...left[ \begin{array}{cc}
1 & 0 \\
0 & 1
\end{array} \right]
\end{displaymath}](img399.png) |
(4.174) |
となりright inverseを満足する。
![\begin{displaymath}
\mbox{\boldmath$A$}^R\mbox{\boldmath$b$} = \left[ \begin{ar...
...\left[ \begin{array}{r}
9 \\
-3 \\
3
\end{array} \right]
\end{displaymath}](img400.png) |
(4.175) |
![\begin{displaymath}
\mbox{\boldmath$A$}^R\mbox{\boldmath$A$} = \left[ \begin{ar...
...1 & 4 & 4 \\
0 & -1 & -2 \\
0 & 1 & 2
\end{array} \right]
\end{displaymath}](img401.png) |
(4.176) |
![\begin{displaymath}
( \mbox{\boldmath$I$}_m - \mbox{\boldmath$A$}^R\mbox{\boldm...
... & -4 \\
0 & 2 & 2 \\
0 & -1 & -1 \\
\end{array} \right]
\end{displaymath}](img402.png) |
(4.177) |
![\begin{displaymath}
\left[ \begin{array}{c}
x_1 \\
x_2 \\
x_3
\end{array}...
...y_2-4y_3 \\
2y_2+2y_3 \\
-y_2-y_3 \\
\end{array} \right]
\end{displaymath}](img403.png) |
(4.178) |
いま
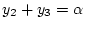 とすると
とすると
![\begin{displaymath}
\left[ \begin{array}{c}
x_1 \\
x_2 \\
x_3
\end{array}...
...pha \\
-3 + 2\alpha \\
3 - \alpha \\
\end{array} \right]
\end{displaymath}](img405.png) |
(4.179) |
となり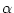 についての無限の解が得られる。
についての無限の解が得られる。
上記のごとく非正方逆行列は無数存在するので、その中から
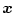 の解を
最小にする場合を求める。すなわち(4.172)式の一般解を用いて
の解を
最小にする場合を求める。すなわち(4.172)式の一般解を用いて
![\begin{displaymath}
\Vert \mbox{\boldmath$x$} \Vert = \sum_{i=1}^{m}(x_{0i})^2 ...
...x{\boldmath$A$}^R\mbox{\boldmath$A$})\mbox{\boldmath$y$}\Vert]
\end{displaymath}](img407.png) |
(4.180) |
とし、上式が最小となるように
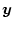 を定める。すなわち
を定める。すなわち
![\begin{displaymath}
\Vert\mbox{\boldmath$x$}\Vert = [\mbox{\boldmath$A$}^R\mbox...
...-\mbox{\boldmath$A$}^R\mbox{\boldmath$A$})\mbox{\boldmath$y$}]
\end{displaymath}](img408.png) |
(4.181) |
とし
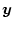 で偏微分し
で偏微分し
![\begin{displaymath}
\frac{\partial \Vert\mbox{\boldmath$x$}\Vert}{\partial \mbox...
...-\mbox{\boldmath$A$}^R\mbox{\boldmath$A$})\mbox{\boldmath$y$}]
\end{displaymath}](img409.png) |
(4.182) |
これを0とするときの
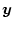 を
を
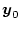 とした場合
とした場合
![\begin{displaymath}
(\mbox{\boldmath$I$}_m-\mbox{\boldmath$A$}^R\mbox{\boldmath$...
...x{\boldmath$A$}^R\mbox{\boldmath$A$})\mbox{\boldmath$y$}_0] =0
\end{displaymath}](img411.png) |
(4.183) |
となる。いま(4.181)式が最小となる場合の
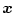 を
を
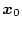 とし、
その場合の
とし、
その場合の
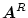 を
を
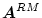 としたとき
としたとき
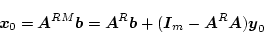 |
(4.184) |
となる。この両辺に
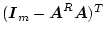 を左から掛けると
を左から掛けると
![\begin{displaymath}
(\mbox{\boldmath$I$}_m-\mbox{\boldmath$A$}^R\mbox{\boldmath...
...{\boldmath$A$}^R\mbox{\boldmath$A$})\mbox{\boldmath$y$}_0] = 0
\end{displaymath}](img416.png) |
(4.185) |
となる。したがって
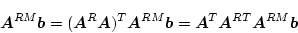 |
(4.186) |
と書ける。両辺に前から
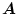 を掛けると
を掛けると
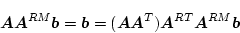 |
(4.187) |
となり、これより
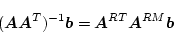 |
(4.188) |
となるので、これを再び(4.187)式の右辺に代入すると
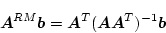 |
(4.189) |
となって
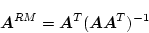 |
(4.190) |
の関係が得られる。これは
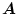 が
が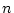 の階数のときの最小非正方逆行列であり、
これをPseudo Inverseともいう。
の階数のときの最小非正方逆行列であり、
これをPseudo Inverseともいう。
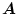 が
が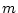 の階数のときは
の階数のときは
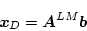 |
(4.191) |
とし、
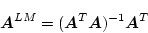 |
(4.192) |
より最小非正方逆行列が得られる。
[例]前例における最小値を求める。
であるから
![\begin{displaymath}
\mbox{\boldmath$A$}\mbox{\boldmath$A$}^T = \left[ \begin{ar...
...left[ \begin{array}{cc}
5 & 2 \\
2 & 5
\end{array} \right]
\end{displaymath}](img425.png) |
(4.193) |
![\begin{displaymath}[ \mbox{\boldmath$A$}\mbox{\boldmath$A$}^T]^{-1} = \frac{1}{2...
...2}{21} \\
\frac{-2}{21} & \frac{5}{21}
\end{array} \right]
\end{displaymath}](img426.png) |
(4.194) |
![\begin{displaymath}
\mbox{\boldmath$A$}^{RM} = \left[ \begin{array}{cc}
1 & 0 ...
...}{21} \\
\frac{-4}{21} & \frac{10}{21}
\end{array} \right]
\end{displaymath}](img427.png) |
(4.195) |
となり
![\begin{displaymath}
\mbox{\boldmath$x$}_0 = \mbox{\boldmath$A$}^{RM}\mbox{\bold...
...c{3}{9} \\
\frac{9}{7} \\
\frac{6}{7}
\end{array} \right]
\end{displaymath}](img428.png) |
(4.196) |
が最小値である。前例の結果の(4.180)式より
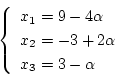 |
(4.197) |
を用いて
とし、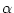 に対する
に対する
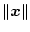 の最小値を求めると
の最小値を求めると
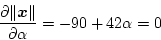 |
(4.199) |
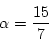 |
(4.200) |
となるので、これを(4.196)式に代入すると
![\begin{displaymath}
\left[ \begin{array}{c}
x_1 \\
x_2 \\
x_3
\end{array}...
...c{3}{7} \\
\frac{9}{7} \\
\frac{6}{7}
\end{array} \right]
\end{displaymath}](img436.png) |
(4.201) |
となって、(4.197)式と同一の結果が得られる。
(4.162)式で示したように、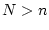 のときは
のときは
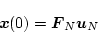 |
(4.202) |
で表される。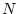 サンプリングで状態ベクトルを0とする最小の
サンプリングで状態ベクトルを0とする最小の
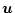 を
を
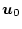 とした場合、この式は(4.164)式に対応し、
とした場合、この式は(4.164)式に対応し、
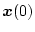 が
が
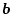 に、
に、
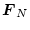 が
が
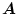 に、
に、
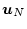 が
が
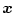 に相当する。したがっ
て、(4.158)式で定義したエネルギを最小にする制御は
に相当する。したがっ
て、(4.158)式で定義したエネルギを最小にする制御は
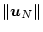 を最小にする
を最小にする
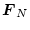 の逆行列の問題となり、(4.191)式より
の逆行列の問題となり、(4.191)式より
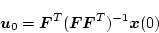 |
(4.203) |
より求められる。そのときの制御エネルギは
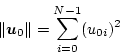 |
(4.204) |
である。もし任意のに対して最小エネルギ制御をしようとするならば、
図4.19のような制御器を用いればよい。
図 4.19:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-6-1.eps} \end{center} \end{figure}](img443.png) |
[例]いま4.6節(1)項の例で与えられたシステム
![\begin{displaymath}
\mbox{\boldmath$x$}(k+1) =
\left[
\begin{array}{cc}
1 & ...
...[
\begin{array}{c}
0.368 \\
0.632
\end{array} \right]u(k)
\end{displaymath}](img353.png) |
(4.205) |
の最小エネルギ制御を求める。
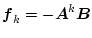 の
の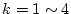 を適用して
を適用して
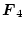 を求めると
を求めると
![\begin{displaymath}
\mbox{\boldmath$F$}_4 = \left[ \begin{array}{rrrr}
0.717 &...
... \\
-1.717 & -4.671 & -12.696 & -34.513
\end{array} \right]
\end{displaymath}](img447.png) |
(4.206) |
となる。これより
![\begin{displaymath}
\mbox{\boldmath$F$}_4\mbox{\boldmath$F$}_4^T = \left[ \begi...
...}
1273.9 & -1323.5 \\
-1323.5 & 1377.1
\end{array} \right]
\end{displaymath}](img448.png) |
(4.207) |
![\begin{displaymath}
(\mbox{\boldmath$F$}_4\mbox{\boldmath$F$}_4^T)^{-1} = \left...
...cc}
0.5225 & 0.5022 \\
0.5022 & 0.4833
\end{array} \right]
\end{displaymath}](img449.png) |
(4.208) |
が得られ
![\begin{displaymath}
\mbox{\boldmath$F$}^{RM} = \mbox{\boldmath$F$}_4^T(\mbox{\b...
...0.2643 & -0.2632 \\
0.1794 & 0.1473 \\
\end{array} \right]
\end{displaymath}](img450.png) |
(4.209) |
となる。したっがて最小エネルギ制御の為の入力は
![\begin{displaymath}
\left[ \begin{array}{c}
u(0) \\
u(1) \\
u(2) \\
u(3)...
...eft[ \begin{array}{c}
x_1(0) \\
x_2(0)
\end{array} \right]
\end{displaymath}](img451.png) |
(4.210) |
となり、もし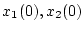 が
が
![\begin{displaymath}
\left[ \begin{array}{c}
x_1(0) \\
x_2(0)
\end{array} \r...
... \begin{array}{r}
-40.9067 \\
43.5067
\end{array} \right]
\end{displaymath}](img452.png) |
(4.211) |
で与えられたとき
![\begin{displaymath}
\left[ \begin{array}{c}
u(0) \\
u(1) \\
u(2) \\
u(3)...
...63 \\
-0.5352 \\
-0.6408 \\
-0.9277
\end{array} \right]
\end{displaymath}](img453.png) |
(4.212) |
が各サンプリングごとに加える制御入力となり
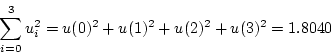 |
(4.213) |
がエネルギである。
同様にして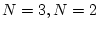 について求めると
について求めると
![\begin{displaymath}
\left[ \begin{array}{c}
u(0) \\
u(1) \\
u(2)
\end{ar...
...ay}{r}
1.0732 \\
-0.1602 \\
-3.5230
\end{array} \right]
\end{displaymath}](img456.png) |
(4.214) |
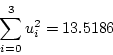 |
(4.215) |
![\begin{displaymath}
\left[ \begin{array}{c}
u(0) \\
u(1)
\end{array} \righ...
...
\begin{array}{r}
10.6225 \\
-13.2225
\end{array} \right]
\end{displaymath}](img458.png) |
(4.216) |
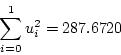 |
(4.217) |
となる。以上より、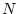 を
を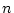 に近くとるほど全エネルギが大きくなり、また
に近くとるほど全エネルギが大きくなり、また
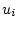 も大きくなる。したがって
も大きくなる。したがって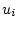 に制限がある場合には、
に制限がある場合には、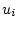 が制限値を
越えないように
が制限値を
越えないように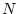 の値を増大させる。前例で
の値を増大させる。前例で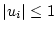 と制限したときは
と制限したときは
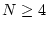 となる。
となる。


Next: 有限時間整定法
Up: 離散値系の各種制御法
Previous: レギュレータ問題
Yasunari SHIDAMA
平成15年6月30日
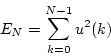
![]() の場合は目標値には到達できない。その時は目標値と最終状態変数との差、
すなわち誤差ベクトルの測度
の場合は目標値には到達できない。その時は目標値と最終状態変数との差、
すなわち誤差ベクトルの測度
![]() は
は![]() の非正方行列である。したがって
の非正方行列である。したがって
![]() を求めるためには
非正方行列の逆行列を求めなければならない。
を求めるためには
非正方行列の逆行列を求めなければならない。
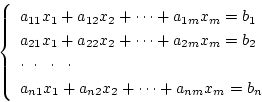
![\begin{displaymath}
\mbox{\boldmath$A$} = \left[ \begin{array}{cccc}
a_{11} & ...
...y}{c}
b_1 \\
b_2 \\
\vdots \\
b_n
\end{array} \right]
\end{displaymath}](img375.png)
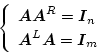
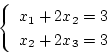
![\begin{displaymath}
\mbox{\boldmath$A$} = \left[ \begin{array}{ccc}
1 & 2 & 0 ...
...h$b$} = \left[ \begin{array}{c}
3 \\
3
\end{array} \right]
\end{displaymath}](img397.png)
![\begin{displaymath}
\mbox{\boldmath$A$}^R = \left[ \begin{array}{cr}
1 & 2 \\
0 & -1 \\
0 & 1
\end{array} \right]
\end{displaymath}](img398.png)
![\begin{displaymath}
\mbox{\boldmath$A$}\mbox{\boldmath$A$}^R = \left[ \begin{ar...
...left[ \begin{array}{cc}
1 & 0 \\
0 & 1
\end{array} \right]
\end{displaymath}](img399.png)
![\begin{displaymath}
\mbox{\boldmath$A$}^R\mbox{\boldmath$b$} = \left[ \begin{ar...
...\left[ \begin{array}{r}
9 \\
-3 \\
3
\end{array} \right]
\end{displaymath}](img400.png)
![\begin{displaymath}
\mbox{\boldmath$A$}^R\mbox{\boldmath$A$} = \left[ \begin{ar...
...1 & 4 & 4 \\
0 & -1 & -2 \\
0 & 1 & 2
\end{array} \right]
\end{displaymath}](img401.png)
![\begin{displaymath}
( \mbox{\boldmath$I$}_m - \mbox{\boldmath$A$}^R\mbox{\boldm...
... & -4 \\
0 & 2 & 2 \\
0 & -1 & -1 \\
\end{array} \right]
\end{displaymath}](img402.png)
![\begin{displaymath}
\left[ \begin{array}{c}
x_1 \\
x_2 \\
x_3
\end{array}...
...y_2-4y_3 \\
2y_2+2y_3 \\
-y_2-y_3 \\
\end{array} \right]
\end{displaymath}](img403.png)
![]() が
が![]() の階数のときは
の階数のときは
![\begin{displaymath}
\mbox{\boldmath$A$} = \left[ \begin{array}{ccc}
1 & 2 & 0 ...
...h$b$} = \left[ \begin{array}{c}
3 \\
3
\end{array} \right]
\end{displaymath}](img397.png)
![\begin{displaymath}
\mbox{\boldmath$A$}\mbox{\boldmath$A$}^T = \left[ \begin{ar...
...left[ \begin{array}{cc}
5 & 2 \\
2 & 5
\end{array} \right]
\end{displaymath}](img425.png)
![\begin{displaymath}[ \mbox{\boldmath$A$}\mbox{\boldmath$A$}^T]^{-1} = \frac{1}{2...
...2}{21} \\
\frac{-2}{21} & \frac{5}{21}
\end{array} \right]
\end{displaymath}](img426.png)
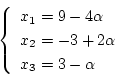
![\begin{displaymath}
\left[ \begin{array}{c}
x_1 \\
x_2 \\
x_3
\end{array}...
...c{3}{7} \\
\frac{9}{7} \\
\frac{6}{7}
\end{array} \right]
\end{displaymath}](img436.png)
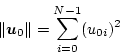
![\begin{displaymath}
\mbox{\boldmath$x$}(k+1) =
\left[
\begin{array}{cc}
1 & ...
...[
\begin{array}{c}
0.368 \\
0.632
\end{array} \right]u(k)
\end{displaymath}](img353.png)
![]() の
の![]() を適用して
を適用して
![]() を求めると
を求めると
![\begin{displaymath}
\mbox{\boldmath$F$}_4 = \left[ \begin{array}{rrrr}
0.717 &...
... \\
-1.717 & -4.671 & -12.696 & -34.513
\end{array} \right]
\end{displaymath}](img447.png)
![\begin{displaymath}
\mbox{\boldmath$F$}_4\mbox{\boldmath$F$}_4^T = \left[ \begi...
...}
1273.9 & -1323.5 \\
-1323.5 & 1377.1
\end{array} \right]
\end{displaymath}](img448.png)
![\begin{displaymath}
(\mbox{\boldmath$F$}_4\mbox{\boldmath$F$}_4^T)^{-1} = \left...
...cc}
0.5225 & 0.5022 \\
0.5022 & 0.4833
\end{array} \right]
\end{displaymath}](img449.png)
![\begin{displaymath}
\mbox{\boldmath$F$}^{RM} = \mbox{\boldmath$F$}_4^T(\mbox{\b...
...0.2643 & -0.2632 \\
0.1794 & 0.1473 \\
\end{array} \right]
\end{displaymath}](img450.png)
![\begin{displaymath}
\left[ \begin{array}{c}
u(0) \\
u(1) \\
u(2) \\
u(3)...
...eft[ \begin{array}{c}
x_1(0) \\
x_2(0)
\end{array} \right]
\end{displaymath}](img451.png)
![\begin{displaymath}
\left[ \begin{array}{c}
x_1(0) \\
x_2(0)
\end{array} \r...
... \begin{array}{r}
-40.9067 \\
43.5067
\end{array} \right]
\end{displaymath}](img452.png)
![\begin{displaymath}
\left[ \begin{array}{c}
u(0) \\
u(1) \\
u(2) \\
u(3)...
...63 \\
-0.5352 \\
-0.6408 \\
-0.9277
\end{array} \right]
\end{displaymath}](img453.png)
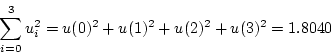
![]() について求めると
について求めると
![\begin{displaymath}
\left[ \begin{array}{c}
u(0) \\
u(1) \\
u(2)
\end{ar...
...ay}{r}
1.0732 \\
-0.1602 \\
-3.5230
\end{array} \right]
\end{displaymath}](img456.png)
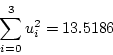
![\begin{displaymath}
\left[ \begin{array}{c}
u(0) \\
u(1)
\end{array} \righ...
...
\begin{array}{r}
10.6225 \\
-13.2225
\end{array} \right]
\end{displaymath}](img458.png)