


Next: 最小エネルギ制御
Up: 離散値系の各種制御法
Previous: 離散値系の各種制御法
レギュレータ問題
いまレギュレータ問題として、任意の初期条件
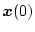 から、目標値
から、目標値
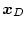 に
有限時間で到達させるのに、どのような入力を加えたらよいかという問題を考え
る。
に
有限時間で到達させるのに、どのような入力を加えたらよいかという問題を考え
る。
システム方程式を
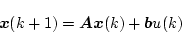 |
(4.143) |
の単入力系とする。もしこのシステムが可制御であれば、4.4節
(4)項で述べたように
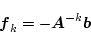 |
(4.144) |
としたとき、ベクトルの組
![$[\mbox{\boldmath$f$}_1,\mbox{\boldmath$f$}_2,\cdots,\mbox{\boldmath$f$}_N]$](img332.png) のうち
のうち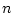 個の
線形独立なベクトルが存在する。
個の
線形独立なベクトルが存在する。
いま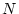 サンプリングの時の状態変数は(4.111)式より
サンプリングの時の状態変数は(4.111)式より
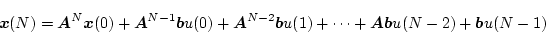 |
(4.145) |
である。これが目標値となるためには
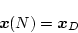 |
(4.146) |
でなければならない。(4.147)式の両辺に
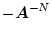 を掛ける
と
を掛ける
と
となる。ここに
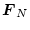 は
は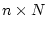 マトリクスである。もし
マトリクスである。もし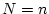 で可制御
ならば
で可制御
ならば
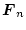 は特異行列とはならないから逆行列が可能である。したがって
は特異行列とはならないから逆行列が可能である。したがって
![\begin{displaymath}
\mbox{\boldmath$u$}_n=\mbox{\boldmath$F$}_n^{-1}[\mbox{\boldmath$x$}(0)-\mbox{\boldmath$A$}^{-n}\mbox{\boldmath$x$}_D]
\end{displaymath}](img345.png) |
(4.150) |
が得られる。このような
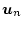 、すなわち
、すなわち
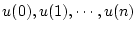 を加えれ
ば目標値に到達させることができる。
を加えれ
ば目標値に到達させることができる。
もし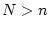 の場合には
の場合には
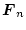 は非正方行列となり、
は非正方行列となり、
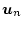 は一意ではなく
なる。したがって他の拘束条件(例えば入力の制御等)を加えることができる。
は一意ではなく
なる。したがって他の拘束条件(例えば入力の制御等)を加えることができる。
[例]与えられたプラントの連続系状態方程式を
![\begin{displaymath}
\dot{\mbox{\boldmath$x$}}(t) =
\left[
\begin{array}{cc}
...
...+
\left[
\begin{array}{c}
0 \\
1
\end{array} \right]u(t)
\end{displaymath}](img349.png) |
(4.151) |
とし、初期値
![$\mbox{\boldmath$x$}(0) = \displaystyle\left[ \begin{array}{c}
x_1(0) \\
x_2(0)
\end{array} \right] $](img350.png) から、目標値
から、目標値
![$\mbox{\boldmath$x$}_D = \displaystyle\left[ \begin{array}{c}
0 \\
0
\end{array} \right]$](img351.png) に到達させる場合を考える。ただしサンプリング周期
に到達させる場合を考える。ただしサンプリング周期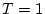 秒の場合とする。
秒の場合とする。
ホールド回路と結合した場合の離散値系の状態方程式は4.3節(2)項の手法により
![\begin{displaymath}
\mbox{\boldmath$x$}(k+1) =
\left[
\begin{array}{cc}
1 & ...
...[
\begin{array}{c}
0.368 \\
0.632
\end{array} \right]u(k)
\end{displaymath}](img353.png) |
(4.152) |
となる。二次系なので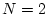 とし(4.145)式の
とし(4.145)式の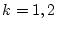 について求めると
について求めると
となるので
となる。ゆえに(4.151)式の
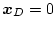 として
として
![\begin{displaymath}
\left[
\begin{array}{c}
u(0) \\
u(1)
\end{array} \righ...
...ft[
\begin{array}{c}
x_1(0) \\
x_2(0)
\end{array} \right]
\end{displaymath}](img361.png) |
(4.155) |
が求める入力である。
もし上例で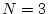 とした場合
とした場合
が加わり、(4.150)式は
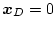 の場合
の場合
![\begin{displaymath}
\left[ \begin{array}{c}
x_1(0) \\
x_2(0)
\end{array} \...
...begin{array}{c}
u(0) \\
u(1) \\
u(2)
\end{array} \right]
\end{displaymath}](img364.png) |
(4.156) |
となる。
この式は二つの式に対して未知数が三つあるので、一つの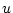 は任意に定めるこ
とができる。このように
は任意に定めるこ
とができる。このように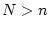 の場合はそれだけ他の条件を加えて
の場合はそれだけ他の条件を加えて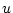 を決定
することができる。
を決定
することができる。



Next: 最小エネルギ制御
Up: 離散値系の各種制御法
Previous: 離散値系の各種制御法
Yasunari SHIDAMA
平成15年6月30日
![]() サンプリングの時の状態変数は(4.111)式より
サンプリングの時の状態変数は(4.111)式より
![]() の場合には
の場合には
![]() は非正方行列となり、
は非正方行列となり、
![]() は一意ではなく
なる。したがって他の拘束条件(例えば入力の制御等)を加えることができる。
は一意ではなく
なる。したがって他の拘束条件(例えば入力の制御等)を加えることができる。
![\begin{displaymath}
\dot{\mbox{\boldmath$x$}}(t) =
\left[
\begin{array}{cc}
...
...+
\left[
\begin{array}{c}
0 \\
1
\end{array} \right]u(t)
\end{displaymath}](img349.png)
![$\mbox{\boldmath$x$}(0) = \displaystyle\left[ \begin{array}{c}
x_1(0) \\
x_2(0)
\end{array} \right] $](img350.png) から、目標値
から、目標値
![$\mbox{\boldmath$x$}_D = \displaystyle\left[ \begin{array}{c}
0 \\
0
\end{array} \right]$](img351.png) に到達させる場合を考える。ただしサンプリング周期
に到達させる場合を考える。ただしサンプリング周期![\begin{displaymath}
\mbox{\boldmath$x$}(k+1) =
\left[
\begin{array}{cc}
1 & ...
...[
\begin{array}{c}
0.368 \\
0.632
\end{array} \right]u(k)
\end{displaymath}](img353.png)
![\begin{eqnarray*}
\mbox{\boldmath$f$}_1 & = & -\mbox{\boldmath$A$}^{-1}\mbox{\b...
... \left[ \begin{array}{r}
3.672 \\
-4.671
\end{array} \right]
\end{eqnarray*}](img356.png)
![$\displaystyle \left[
\begin{array}{cc}
\mbox{\boldmath$f$}_1 & \mbox{\boldmath$...
...=
\left[
\begin{array}{rr}
0.718 & 3.671 \\
-1.718 & -4.671
\end{array}\right]$](img358.png)
![$\displaystyle \left[
\begin{array}{rr}
-1.582 & -1.243 \\
0.582 & 0.243
\end{array}\right]$](img360.png)
![\begin{displaymath}
\left[
\begin{array}{c}
u(0) \\
u(1)
\end{array} \righ...
...ft[
\begin{array}{c}
x_1(0) \\
x_2(0)
\end{array} \right]
\end{displaymath}](img361.png)
![]() とした場合
とした場合
![\begin{displaymath}
\mbox{\boldmath$f$}_3 =
-\mbox{\boldmath$A$}^{-3}\mbox{\bo...
...t[
\begin{array}{r}
11.696 \\
-12.696
\end{array} \right]
\end{displaymath}](img363.png)
![\begin{displaymath}
\left[ \begin{array}{c}
x_1(0) \\
x_2(0)
\end{array} \...
...begin{array}{c}
u(0) \\
u(1) \\
u(2)
\end{array} \right]
\end{displaymath}](img364.png)
![]() は任意に定めるこ
とができる。このように
は任意に定めるこ
とができる。このように![]() の場合はそれだけ他の条件を加えて
の場合はそれだけ他の条件を加えて![]() を決定
することができる。
を決定
することができる。