


Next: 最適制御理論
Up: 離散値系の各種制御法
Previous: 有限時間整定法
極配置制御(Pole assignment)
制御系に望ましい固有値をもたせるようにフィードバックゲインを定める方法を
極配置法という。
いまシステム方程式を
とする。フィードバック
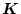 を用いて
を用いて
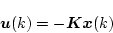 |
(4.252) |
のように構成すると
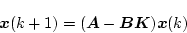 |
(4.253) |
となり、特性方程式は
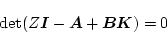 |
(4.254) |
のようになる。
単入力系の場合は、状態変数を直接法(可制御正準形式)に変換して
![\begin{displaymath}
\mbox{\boldmath$x$}(k+1) = \left[ \begin{array}{cccc}
0 & ...
...rray}{c}
0 \\
\vdots \\
0 \\
1
\end{array} \right]u(k)
\end{displaymath}](img532.png) |
(4.255) |
のように表示し
![\begin{displaymath}
\mbox{\boldmath$K$} = \left[ \begin{array}{cccc}
K_n & K_{n-1} & \cdots & K_1
\end{array} \right]
\end{displaymath}](img533.png) |
(4.256) |
とすれば(4.255)式は次のようになる。
もし指定したい極を
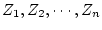 としたとき
としたとき
![\begin{displaymath}
\det[Z\mbox{\boldmath$I$}-\mbox{\boldmath$A$}+\mbox{\boldmath$BK$}] = (Z-Z_1)(Z-Z_2)\cdots(Z-Z_n)
\end{displaymath}](img538.png) |
(4.258) |
として(4.258)式と等値とすれば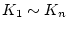 が決定できる。
が決定できる。
この方法の場合、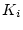 は特性方程式の1つの係数
は特性方程式の1つの係数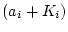 の所にしか入っ
ていないので、
の所にしか入っ
ていないので、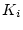 の変化は他の係数には影響を与えない。したがって、
の変化は他の係数には影響を与えない。したがって、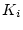 の変化の効果が直接的に観察できる利点がある。
の変化の効果が直接的に観察できる利点がある。
多入力の場合にも、上記の方法が適用できるが、その場合には
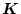 は一意的
ではない。
は一意的
ではない。
多入力の場合で、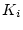 を変化させたとき他の固有値に影響を与えず、特定の固
有値
を変化させたとき他の固有値に影響を与えず、特定の固
有値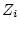 のみを直接的に変更する方法にModel State Control (モード状態制
御)がある。この方法では状態変数を対角形(Diagonal Form)の状態変数
のみを直接的に変更する方法にModel State Control (モード状態制
御)がある。この方法では状態変数を対角形(Diagonal Form)の状態変数
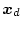 にとる必要がある。そのため任意の状態変数
にとる必要がある。そのため任意の状態変数
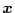 から変換行列
から変換行列
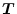 を用いて次のように変換する。
を用いて次のように変換する。
すなわち
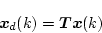 |
(4.259) |
と表す。そのときシステム方程式は
で表される。この場合
である。
もとのシステムの特性方程式は
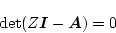 |
(4.265) |
であり、変換後のシステムの特性方程式は
となって、
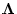 の対角要素
の対角要素
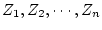 は両システム共通の
固有値であることがわかる。
は両システム共通の
固有値であることがわかる。
(4.263)式より
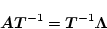 |
(4.267) |
となる。ここで
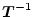 を各列ベクトルで表して
を各列ベクトルで表して
![\begin{displaymath}
\mbox{\boldmath$T$}^{-1} = \left[ \begin{array}{cccc}
\mbo...
...h$v$}_2 & \cdots & \mbox{\boldmath$v$}_n
\end{array} \right]
\end{displaymath}](img563.png) |
(4.268) |
とし、(4.268)式に代入すると
![\begin{displaymath}
\mbox{\boldmath$A$}\left[ \begin{array}{cccc}
\mbox{\boldm...
..._2 & & \\
& & \ddots & \\
0 & & & Z_n
\end{array} \right]
\end{displaymath}](img564.png) |
(4.269) |
となり、各列は
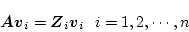 |
(4.270) |
また
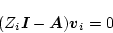 |
(4.271) |
で表される。この式は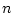 個の要素で構成される未知ベクトル
個の要素で構成される未知ベクトル
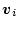 が
が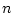 個
あって、方程式が
個
あって、方程式が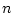 個であるから、
個であるから、
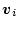 には一意の解はない。したっがて
大きさは定まらないが、普通方向は確立する。これを
には一意の解はない。したっがて
大きさは定まらないが、普通方向は確立する。これを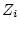 に対する固有ベクト
ル(Eigen vector)という。大きさを
に対する固有ベクト
ル(Eigen vector)という。大きさを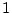 にとった場合、すなわち
にとった場合、すなわち
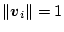 にした場合を正規固有ベクトル(Normal Eigenvector)という。
にした場合を正規固有ベクトル(Normal Eigenvector)という。
(4.272)式から適当な固有ベクトルを定めれば
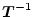 が得られる。
この
が得られる。
この
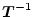 のこ、とを法行列(Model matrix)という。
のこ、とを法行列(Model matrix)という。
(4.261)式において
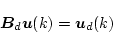 |
(4.272) |
とおくと
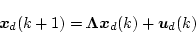 |
(4.273) |
となる。いまこの
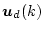 をフィードバックで構成するとして
をフィードバックで構成するとして
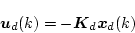 |
(4.274) |
とおくと、(4.274)式は
![\begin{displaymath}
\mbox{\boldmath$x$}_d(k+1) = [\mbox{\boldmath$\Lambda$}-\mbox{\boldmath$K$}_d]\mbox{\boldmath$x$}_d(k)
\end{displaymath}](img574.png) |
(4.275) |
となる。もしこの
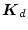 も対角形で
も対角形で
![\begin{displaymath}
\mbox{\boldmath$K$}_d = \left[ \begin{array}{cccc}
k_{d1} ...
...& & \\
& & \ddots & \\
0 & & & k_{dn}
\end{array} \right]
\end{displaymath}](img576.png) |
(4.276) |
であるなら、(4.276)式の特性方程式は
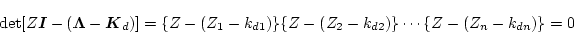 |
(4.277) |
となり、
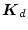 の選択により、任意の固有値を設定することができることに
なる。
の選択により、任意の固有値を設定することができることに
なる。
しかしながら、実際の系を構成する場合には
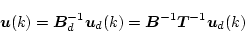 |
(4.278) |
として、図4.21のようにする必要がある。
図 4.21:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-6-3.eps} \end{center} \end{figure}](img579.png) |
このとき
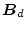 の逆行列は
の逆行列は
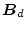 が正則でなければ求められない。したがっ
て、この方法では入力の次数がシステムの次数に等しい場合にのみ限られる。
が正則でなければ求められない。したがっ
て、この方法では入力の次数がシステムの次数に等しい場合にのみ限られる。
もしシステムが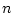 次で、入力が
次で、入力が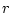 次の場合は
次の場合は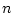 個の固有値のうち
個の固有値のうち
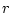 個の固有値については上記の方法を用いて変えられる。
個の固有値については上記の方法を用いて変えられる。
すなわち
とし、
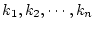 のうち
のうち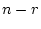 個は0にとる。
例えば
個は0にとる。
例えば
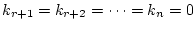 とし、
とし、
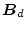 の要素を全部1になるようにとったとき
の要素を全部1になるようにとったとき
となるので、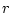 個の固有値は
個の固有値は
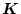 のとりかたで直接的に変えることができる。
のとりかたで直接的に変えることができる。
[例]システム方程式を次とする。
![\begin{displaymath}
\mbox{\boldmath$x$}(k+1) =
\left[
\begin{array}{cc}
1 & ...
...[
\begin{array}{c}
0.368 \\
0.632
\end{array} \right]u(k)
\end{displaymath}](img353.png) |
(4.281) |
この場合の特性方程式
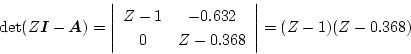 |
(4.282) |
より固有値は
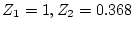 となる。(4.270)式より
となる。(4.270)式より
![\begin{displaymath}
\left[ \begin{array}{cc}
1 & 0.632 \\
0 & 0.368
\end{ar...
...[ \begin{array}{cc}
1 & 0 \\
0 & 0.368
\end{array} \right]
\end{displaymath}](img593.png) |
(4.283) |
とすると
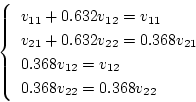 |
(4.284) |
となり、
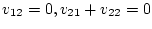 という関係が得られる。
という関係が得られる。
いま
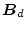 の全要素が1となるように
の全要素が1となるように
![\begin{displaymath}
\mbox{\boldmath$B$}_d = \left[ \begin{array}{c}
1 \\
1
...
...\left[ \begin{array}{c}
0.368 \\
0.632
\end{array} \right]
\end{displaymath}](img596.png) |
(4.285) |
として
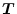 を求めると
を求めると
となる。単入力ゆえ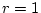 であり
であり
とすると
となる。固有値のうち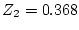 はそのまま残るが、
はそのまま残るが、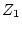 の方は
の方は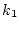 のと
り方で任意に変えることができる。
のと
り方で任意に変えることができる。



Next: 最適制御理論
Up: 離散値系の各種制御法
Previous: 有限時間整定法
Yasunari SHIDAMA
平成15年6月30日
![\begin{displaymath}
\mbox{\boldmath$x$}(k+1) = \left[ \begin{array}{cccc}
0 & ...
...rray}{c}
0 \\
\vdots \\
0 \\
1
\end{array} \right]u(k)
\end{displaymath}](img532.png)
![]() は特性方程式の1つの係数
は特性方程式の1つの係数![]() の所にしか入っ
ていないので、
の所にしか入っ
ていないので、![]() の変化は他の係数には影響を与えない。したがって、
の変化は他の係数には影響を与えない。したがって、![]() の変化の効果が直接的に観察できる利点がある。
の変化の効果が直接的に観察できる利点がある。
![]() は一意的
ではない。
は一意的
ではない。
![]() を変化させたとき他の固有値に影響を与えず、特定の固
有値
を変化させたとき他の固有値に影響を与えず、特定の固
有値![]() のみを直接的に変更する方法にModel State Control (モード状態制
御)がある。この方法では状態変数を対角形(Diagonal Form)の状態変数
のみを直接的に変更する方法にModel State Control (モード状態制
御)がある。この方法では状態変数を対角形(Diagonal Form)の状態変数
![]() にとる必要がある。そのため任意の状態変数
にとる必要がある。そのため任意の状態変数
![]() から変換行列
から変換行列
![]() を用いて次のように変換する。
を用いて次のように変換する。
![]() が得られる。
この
が得られる。
この
![]() のこ、とを法行列(Model matrix)という。
のこ、とを法行列(Model matrix)という。
![\begin{displaymath}
\mbox{\boldmath$K$}_d = \left[ \begin{array}{cccc}
k_{d1} ...
...& & \\
& & \ddots & \\
0 & & & k_{dn}
\end{array} \right]
\end{displaymath}](img576.png)
![]() の逆行列は
の逆行列は
![]() が正則でなければ求められない。したがっ
て、この方法では入力の次数がシステムの次数に等しい場合にのみ限られる。
が正則でなければ求められない。したがっ
て、この方法では入力の次数がシステムの次数に等しい場合にのみ限られる。
![]() 次で、入力が
次で、入力が![]() 次の場合は
次の場合は![]() 個の固有値のうち
個の固有値のうち
![]() 個の固有値については上記の方法を用いて変えられる。
個の固有値については上記の方法を用いて変えられる。
![$\displaystyle \mbox{ただし} \mbox{\boldmath$K$} = \left[ \begin{array}{cccc}
k_1 & & & 0 \\
& k_2 & & \\
& & \ddots & \\
0 & & & k_n
\end{array} \right]$](img584.png)
![\begin{displaymath}
\mbox{\boldmath$x$}(k+1) =
\left[
\begin{array}{cc}
1 & ...
...[
\begin{array}{c}
0.368 \\
0.632
\end{array} \right]u(k)
\end{displaymath}](img353.png)
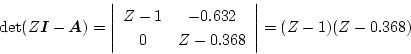
![\begin{displaymath}
\left[ \begin{array}{cc}
1 & 0.632 \\
0 & 0.368
\end{ar...
...[ \begin{array}{cc}
1 & 0 \\
0 & 0.368
\end{array} \right]
\end{displaymath}](img593.png)
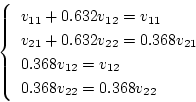
![]() の全要素が1となるように
の全要素が1となるように
![\begin{displaymath}
\mbox{\boldmath$B$}_d = \left[ \begin{array}{c}
1 \\
1
...
...\left[ \begin{array}{c}
0.368 \\
0.632
\end{array} \right]
\end{displaymath}](img596.png)
![\begin{displaymath}\mbox{\boldmath$T$} = \left[ \begin{array}{cc}
1 & 1 \\
0 ...
...gin{array}{cc}
1 & -0.632 \\
0 & 0.632
\end{array} \right]
\end{displaymath}](img597.png)
![$\displaystyle \det \left\{
\left[ \begin{array}{cc}
Z & 0 \\
0 & Z
\end{array}...
...nd{array} \right]
\left[ \begin{array}{cc}
k_1 & 0
\end{array} \right]
\right\}$](img601.png)
![$\displaystyle \det \left[ \begin{array}{cc}
Z-1+k_1 & 0 \\
k_1 & Z-0.368
\end{array} \right] =
(Z-1+k_1)(Z-0.368)$](img602.png)