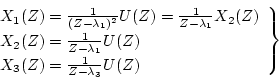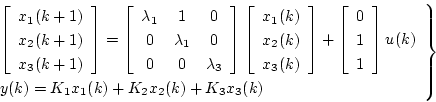Next: 繰り返し法(Iterative Programming)
Up: 状態変数
Previous: Nested Programming
(4.12)式を部分分数に分解すると、次のようになる。
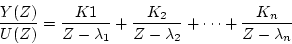 |
(4.35) |
ただし、
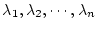 はパルス伝達関数の固有値である。
はパルス伝達関数の固有値である。
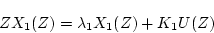 |
(4.36) |
より
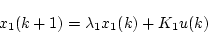 |
(4.37) |
以下同様にして一般的に状態方程式は
![\begin{displaymath}
\left[ \begin{array}{c}
x_1(k+1) \\
x_1(k+1) \\
\vdots ...
...c}
K_1 \\
K_2 \\
\vdots \\
K_n
\end{array} \right]u(k)
\end{displaymath}](img101.png) |
(4.38) |
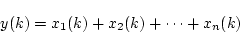 |
(4.39) |
で表される。これをブロック線図で表示すると、図4.7のようになる。
図 4.7:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-2-5.eps} \end{center} \end{figure}](img103.png) |
多重根のある場合は、例えば
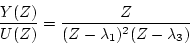 |
(4.40) |
のとき
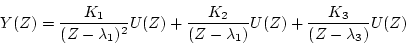 |
(4.41) |
となるから、状態変数を
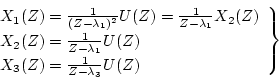 |
(4.42) |
にとれば、状態方程式は
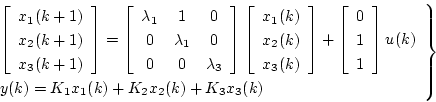 |
(4.43) |
となる。
多重根のある場合のシステムマトリクスは、(a)主対角線は固有値となり、(b)主
対角線の下の要素は全部0、(c)主対角線の上は、二つの等しい固有値の両方に最
も近い所の要素が1(または他の定数)になり、他の要素は0となる。
上例をブロック線図に表示すると図4.8となる。
図 4.8:
![\begin{figure}\begin{center}
\psbox[scale=0.60]{eps/4-2-6.eps} \end{center} \end{figure}](img108.png) |
この部分分数分解法は連続系の正準変数(Jordan形)の場合に類似している。



Next: 繰り返し法(Iterative Programming)
Up: 状態変数
Previous: Nested Programming
Yasunari SHIDAMA
平成15年6月30日
![\begin{displaymath}
\left[ \begin{array}{c}
x_1(k+1) \\
x_1(k+1) \\
\vdots ...
...c}
K_1 \\
K_2 \\
\vdots \\
K_n
\end{array} \right]u(k)
\end{displaymath}](img101.png)