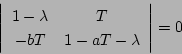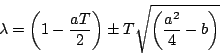

Next: Tustinの方法
Up: 計算機シミュレーション
Previous: 序論
これは状態変数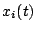 のテーラー展開から近似をする最も簡単な
方法である。
のテーラー展開から近似をする最も簡単な
方法である。
図7.1に示すごとく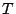 をきざみ幅としたとき
をきざみ幅としたとき
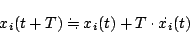 |
(7.4) |
とする。そして
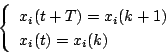 |
(7.5) |
とすれば、
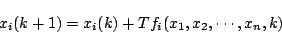 |
(7.6) |
となり、これがEulerの近似である。
[例]
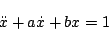 |
(7.7) |
但し
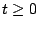
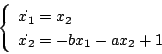 |
(7.8) |
と表示し、Euler近似を用いると
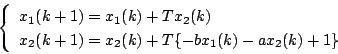 |
(7.9) |
となり、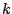 時点から
時点から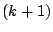 時点が求められる。
時点が求められる。
ここで、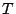 は数値積分に使用するきざみ幅である。
は数値積分に使用するきざみ幅である。
この方法は線形、非線形の両方に使用できるが精度は余り良くない。
(7.9)式をマトリックス表示すると、
![\begin{displaymath}
\left[ \begin{array}{c}
x_1(k+1) \\
x_2(k+1)
\end{array}...
...ight] +
\left[ \begin{array}{c}
0 \\
T
\end{array} \right]
\end{displaymath}](img20.png) |
(7.10) |
となり、これより固有値を求めると
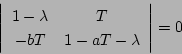 |
(7.11) |
より
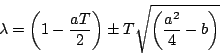 |
(7.12) |
となる。いま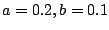 の場合
の場合
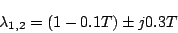 |
(7.13) |
もし、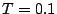 に選ぶと
に選ぶと
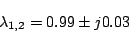 |
(7.14) |
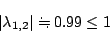 |
(7.15) |
であり、この解は収束する。しかし、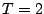 に選ぶと、
に選ぶと、
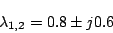 |
(7.16) |
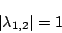 |
(7.17) |
となる。したがって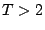 では不安定となり解は発散をする。
このように
では不安定となり解は発散をする。
このように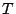 の選択に十分注意を払う必要がある。
の選択に十分注意を払う必要がある。


Next: Tustinの方法
Up: 計算機シミュレーション
Previous: 序論
Yasunari SHIDAMA
平成15年7月29日
![]() をきざみ幅としたとき
をきざみ幅としたとき
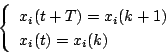
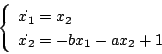
![]() は数値積分に使用するきざみ幅である。
は数値積分に使用するきざみ幅である。
![\begin{displaymath}
\left[ \begin{array}{c}
x_1(k+1) \\
x_2(k+1)
\end{array}...
...ight] +
\left[ \begin{array}{c}
0 \\
T
\end{array} \right]
\end{displaymath}](img20.png)