

Next: Runge-Kuttaの方法
Up: 計算機シミュレーション
Previous: Eulerの方法
この方法は、基本的には微分方程式を差分方程式で近似したものである。
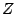 変換の式は
変換の式は
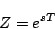 |
(7.18) |
であるから、
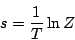 |
(7.19) |
として、これを級数展開すると、
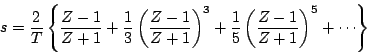 |
(7.20) |
となる。この第一項のみで近似をし
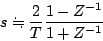 |
(7.21) |
とおいて、連続系の伝達関数を離散値系の伝達関数に置換をして取り扱う
方法である。
[例1]
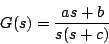 |
(7.22) |
の場合、上式の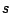 を(7.21)式で置換をし
を(7.21)式で置換をし
として取り扱う。
[例2]
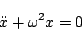 |
(7.24) |
の場合
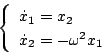 |
(7.25) |
となる。これに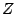 変換の近似式を用いると
変換の近似式を用いると
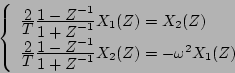 |
(7.26) |
となるので、これを差分方程式で表現すると、
![\begin{displaymath}
\left\{ \begin{array}{l}
x_1(k)=x_1(k-1)+\frac{\displaystyl...
... ^2T}}{\displaystyle{2}}[x_1(k)+x_1(k-1)]
\end{array} \right.
\end{displaymath}](img45.png) |
(7.27) |
両辺より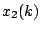 を消去すると
を消去すると
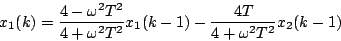 |
(7.28) |
となるので、この式を計算機に適用することができる。


Next: Runge-Kuttaの方法
Up: 計算機シミュレーション
Previous: Eulerの方法
Yasunari SHIDAMA
平成15年7月29日
![]() 変換の式は
変換の式は
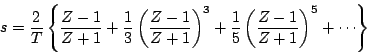
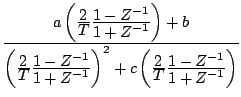
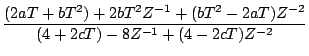
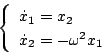
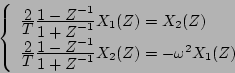
![\begin{displaymath}
\left\{ \begin{array}{l}
x_1(k)=x_1(k-1)+\frac{\displaystyl...
... ^2T}}{\displaystyle{2}}[x_1(k)+x_1(k-1)]
\end{array} \right.
\end{displaymath}](img45.png)