

Next: 各方法の比較
Up: 計算機シミュレーション
Previous: Adams-Moulton Predictor-Corrector法
線形システムのシミュレーションの数値法として状態変数に基づくものが広く用
いられるようになってきた。
すなわち
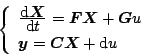 |
(7.40) |
で表されるシステムの入力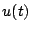 を断片的な定数で等価的に表し
を断片的な定数で等価的に表し
として離散値系の状態方程式
![\begin{displaymath}
\left\{ \begin{array}{l}
\mbox{\boldmath$X$}[(k+1)T]=e^{\mb...
...h$y$}(kT)=\mbox{\boldmath$CX$}(kT)+du(kT)
\end{array} \right.
\end{displaymath}](img89.png) |
(7.41) |
として表され
とすれば
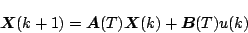 |
(7.42) |
で計算される。
ここで
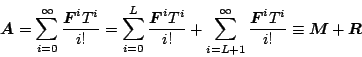 |
(7.43) |
として、
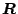 が
が
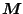 に対して十分小さくなるように
に対して十分小さくなるように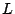 を選択すれば、
を選択すれば、
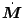 をもって
をもって
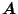 の近似とすることができる。
の近似とすることができる。
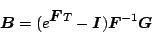 |
(7.44) |
であるから、(7.43)式を代入して
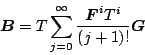 |
(7.45) |
となり、これも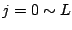 として近似的に求められる。
として近似的に求められる。
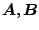 はそれぞれ
はそれぞれ
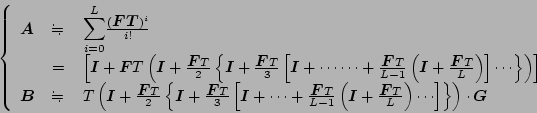 |
(7.46) |
で表されるから、内側の括弧内から計算をするようにすれば、類似の計算の
繰り返しで行なえる。
[例]
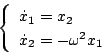 |
(7.47) |
の場合
![\begin{displaymath}
\mbox{\boldmath$F$} = \left[ \begin{array}{cc}
0 & 1 \\
-\omega ^2 & 0
\end{array} \right]
\end{displaymath}](img103.png) |
(7.48) |
ゆえ
![\begin{displaymath}
e^{\mbox{\boldmath$F$}t} =
\left[ \begin{array}{cc}
\cos \o...
...\
-\omega \sin \omega t & \cos \omega t
\end{array} \right]
\end{displaymath}](img104.png) |
(7.49) |
したがって
![\begin{displaymath}
\left[ \begin{array}{c}
x_1(k+1) \\
x_2(k+1)
\end{array}...
...eft[ \begin{array}{c}
x_1(k) \\
x_2(k)
\end{array} \right]
\end{displaymath}](img105.png) |
(7.50) |
となるので、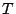 を定めれば計算することができる。
を定めれば計算することができる。


Next: 各方法の比較
Up: 計算機シミュレーション
Previous: Adams-Moulton Predictor-Corrector法
Yasunari SHIDAMA
平成15年7月29日
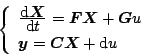
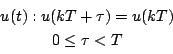
![\begin{displaymath}
\left\{ \begin{array}{l}
\mbox{\boldmath$X$}[(k+1)T]=e^{\mb...
...h$y$}(kT)=\mbox{\boldmath$CX$}(kT)+du(kT)
\end{array} \right.
\end{displaymath}](img89.png)
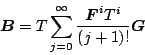
![]() はそれぞれ
はそれぞれ
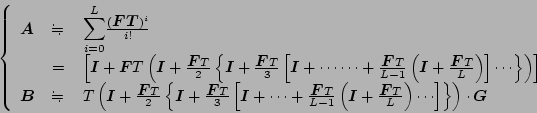
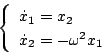
![\begin{displaymath}
\mbox{\boldmath$F$} = \left[ \begin{array}{cc}
0 & 1 \\
-\omega ^2 & 0
\end{array} \right]
\end{displaymath}](img103.png)
![\begin{displaymath}
e^{\mbox{\boldmath$F$}t} =
\left[ \begin{array}{cc}
\cos \o...
...\
-\omega \sin \omega t & \cos \omega t
\end{array} \right]
\end{displaymath}](img104.png)
![\begin{displaymath}
\left[ \begin{array}{c}
x_1(k+1) \\
x_2(k+1)
\end{array}...
...eft[ \begin{array}{c}
x_1(k) \\
x_2(k)
\end{array} \right]
\end{displaymath}](img105.png)