next up previous contents
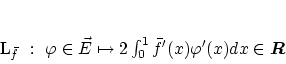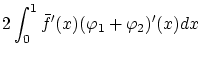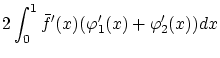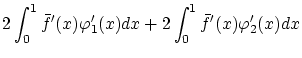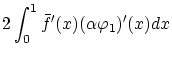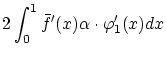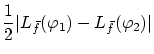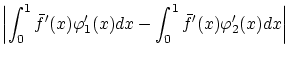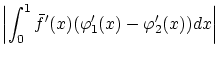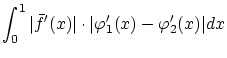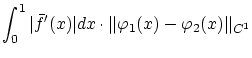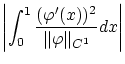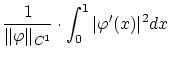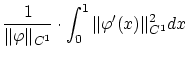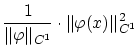
: 微分 : 微分と微分 : アフィン空間 の構造   目次

$L_{\bar{f}}$ の線形性と連続性


\begin{displaymath} % latex2html id marker 849L_{\bar{f}}\ :\ \varphi \in \vec... ...o 2\int_0^1 \bar{f}'(x) \varphi'(x)dx \in \mbox{\boldmath $R$} \end{displaymath}

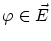は以下に観るように $ \varphi \in \vec{E} $について の線形性と連続性をもっています。
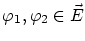$ \varphi_1,\varphi_2 \in \vec{E} $ とすると
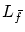$\displaystyle L_{\bar{f}}(\varphi_1 + \varphi_2)$ $\textstyle =$ $\displaystyle 2\int_0^1\bar{f}'(x)(\varphi_1 + \varphi_2)'(x) dx$  
  $\textstyle =$ $\displaystyle 2\int_0^1\bar{f}'(x)(\varphi'_1(x) + \varphi'_2(x))dx$  
  $\textstyle =$ $\displaystyle 2\int_0^1\bar{f}'(x)\varphi'_1(x)dx + 2\int_0^1\bar{f}'(x)\varphi'_2(x)dx$  
  $\textstyle =$ $\displaystyle L_{\bar{f}}(\varphi_1) + L_{\bar{f}}(\varphi_2)$  
$\displaystyle L_{\bar{f}}(\alpha \varphi_1)$ $\textstyle =$ $\displaystyle 2\int_0^1\bar{f}'(x)(\alpha \varphi_1)'(x)dx$  
  $\textstyle =$ $\displaystyle 2\int_0^1\bar{f}'(x)\alpha \cdot \varphi'_1(x)dx$  
  $\textstyle =$ $\displaystyle \alpha L{\bar{f}}(\varphi_1)$  

よって $L_{\bar{f}}$ は 線形です。次に
$\displaystyle \frac{1}{2}\vert L_{\bar{f}}(\varphi_1)-L_{\bar{f}}(\varphi_2)\vert$ $\textstyle =$ $\displaystyle \left\vert\int_0^1 \bar{f}'(x) \varphi'_1(x)dx - \int_0^1 \bar{f}'(x) \varphi'_2(x)dx \right\vert$  
  $\textstyle =$ $\displaystyle \left\vert\int_0^1 \bar{f}'(x) (\varphi'_1(x)-\varphi'_2(x))dx \right\vert$  
  $\textstyle \le$ $\displaystyle \int_0^1 \vert\bar{f}'(x)\vert \cdot \vert\varphi'_1(x)-\varphi'_2(x)\vert dx$  
  $\textstyle \le$ $\displaystyle \int_0^1 \vert\bar{f}'(x)\vert dx \cdot \Vert\varphi_1(x)-\varphi_2(x)\Vert _{C^1}$  
  $\textstyle \le$ $\displaystyle K_{\bar{f}} \Vert\varphi_2 - \varphi_2 \Vert _{C^1}$  

であるから 任意の 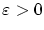$ \varepsilon > 0$について

\begin{displaymath} \delta(\varepsilon) = \frac{\varepsilon}{2K_{\bar{f}}} \end{displaymath}

と選べば，

\begin{displaymath} \Vert\varphi_1 - \varphi_2\Vert _{C^1} < \delta(\varepsilon) \end{displaymath}

なる全ての $\varphi_1 , \varphi_2 \in C^1[0,1]$について

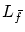\begin{displaymath}\vert L_{\bar{f}}(\varphi_1)-L_{\bar{f}}(\varphi_2)\vert < \varepsilon \end{displaymath}

よって，$L_{\bar{f}}$ は連続です。 最後に残余項の条件，すなわち， 定義式(1.4)の条件

\begin{displaymath} O_1(h) \to 0 \ (\vert h\vert \to 0) \end{displaymath}

について調べてみます。
まず

\begin{displaymath}\int_0^1(\varphi'(x))^2dx = \int_0^1 \frac{(\varphi'(x))^2} {\Vert\varphi\Vert _{C^1}}dx \cdot \Vert\varphi\Vert _{C^1} \end{displaymath}

です。ここで
$\displaystyle \left\vert\int_0^1 \frac{(\varphi'(x))^2}{\Vert\varphi\Vert _{C^1}}dx \right\vert$ $\textstyle \le$ $\displaystyle \frac{1}{\Vert\varphi\Vert _{C^1}} \cdot \int_0^1\vert\varphi'(x)\vert^2dx$  
  $\textstyle \le$ $\displaystyle \frac{1}{\Vert\varphi\Vert _{C^1}} \cdot \int_0^1\Vert\varphi'(x)\Vert^2_{C^1}dx$  
  $\textstyle =$ $\displaystyle \frac{1}{\Vert\varphi\Vert _{C^1}} \cdot \Vert\varphi(x)\Vert^2_{C^1}$  
  $\textstyle =$ $\displaystyle \Vert\varphi\Vert _{C^1} \ \to \ 0 \ (\Vert\varphi\Vert _{C^1}\to 0)$  

よって

\begin{displaymath}O_1 (\varphi) = \int_0^1\frac{(\varphi'(x))^2}{\Vert\varphi\Vert _{C^1}}dx \end{displaymath}

は定義式(1.1)の条件を充たしています。
以上をまとめれば，任意の 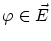$ \varphi \in \vec{E} $に対して

\begin{displaymath}J(\bar{f}+ \varphi) - J(\bar{f}) = L_{\bar{f}} \cdot \varphi + O_1(\varphi)\Vert\varphi\Vert _{C^1} \end{displaymath}

が成立っています。
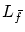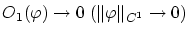
$L_{\bar{f}}$ は 線形かつ連続であり， $O_1(\varphi) \to 0 \ (\Vert\varphi\Vert _{C^1} \to 0)$

next up previous contents
: 微分 : 微分と微分 : アフィン空間 の構造   目次
Yasunari SHIDAMA