


Next: 一般的な4輪移動体の運動学
Up: ある方向にスライドする車輪の場合
Previous: 運動の制御能力
Contents
従来のステアリング車輪の移動体は非ーホロノミック系である.それゆえ,移動体位置と車輪角度置換は関係付けられなかった.Mevanum Wheel の移動体は,ふさわしい運動拘束を導入すればホロノミック拘束となる.そのような場合,移動体位置は車輪回転角から変換して得ることができる.
固定座標系において点Oの位置を決定するために一般座標の 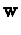 ,
,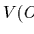 を設定する.もし移動体軸を使い,
を設定する.もし移動体軸を使い,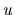 の構成要素
の構成要素 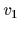 と
と 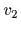 は
は 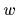 ,
,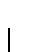 で表すことができる.
で表すことができる.
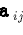 |
(9) |
ここで,係数 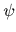 は
は 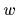 ,
,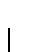 と
と 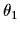 の関数となる.
の関数となる.
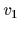 ,
,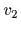 と
と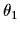 (或いは 式(2.8)に関連する
(或いは 式(2.8)に関連する 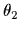 ,
, 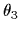 と
と 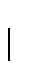 ) が独立であるならば,その移動体系は非ーホロノミックである.点Oの位置座標
) が独立であるならば,その移動体系は非ーホロノミックである.点Oの位置座標 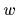 ,
,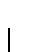 は角度
は角度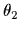 ,
, 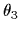 と
と 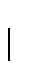 の関数として表すことができない.式(2.8)からわかるように,移動体角位置
の関数として表すことができない.式(2.8)からわかるように,移動体角位置 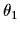 と角度
と角度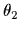 ,
, 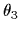 と
と 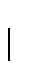 との間に線形の関係があることを得る.
ここで,運動拘束に
との間に線形の関係があることを得る.
ここで,運動拘束に 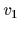 ,
,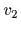 と
と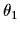 の量を導入すると,次のようになる.
の量を導入すると,次のようになる.
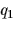 |
(10) |
式(2.9)と(2.10)は,ある場合においてAGV(Automated Guided Vehicle)の重要な因子である 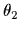 ,
, 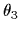 と
と  の関数として,位置座標を得るために統合される.式(2.10)の係数
の関数として,位置座標を得るために統合される.式(2.10)の係数  は位置座標
は位置座標 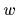 ,
,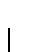 から決定できる.例えば,
から決定できる.例えば,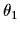 はその位置を決めるための座標軸に並行な軸を保つために選ぶことができる.
最も単純な場合,運動拘束によって次のような関係が得られる.
はその位置を決めるための座標軸に並行な軸を保つために選ぶことができる.
最も単純な場合,運動拘束によって次のような関係が得られる.
または,
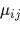 |
(11) |
と表せる.
ここで 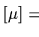 は式(2.8)で定義された行列
は式(2.8)で定義された行列
![$[\mu ]=[ {R_C} ]^{-1}$](img64.gif) の要素である.
もし移動体軸と並行な直交座標
の要素である.
もし移動体軸と並行な直交座標 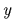 ,
,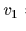 をとるならば,
をとるならば,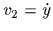 と
と 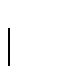 となる.[図2.13(a)].以下の式のように,任意の原点で,位置座標
となる.[図2.13(a)].以下の式のように,任意の原点で,位置座標 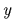 ,
,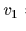 は車輪回転数と関係する.
は車輪回転数と関係する.
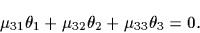 |
(12) |
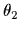 ,
, 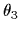 と
と 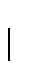 には以下の関係がある.
には以下の関係がある.
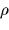 |
(13) |
他方,最も単純な場合を,極座標 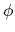
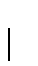 に変換できる.
運動拘束は,以下のようになる.
に変換できる.
運動拘束は,以下のようになる.
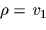 |
(14) |
この場合極座標角 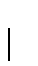 は
は 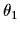 と
と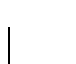 [図2.13(b)と等しくなければならない.以下の式のように,任意の原点で位置座標は車輪回転数と関係がある.
[図2.13(b)と等しくなければならない.以下の式のように,任意の原点で位置座標は車輪回転数と関係がある.
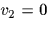 |
(15) |
運動拘束  で,従来の移動体の非ーホロノミックの場合を導き出す.点Oの速度は移動体横軸に沿ってまっすぐとなる.[図2.13(c)]
で,従来の移動体の非ーホロノミックの場合を導き出す.点Oの速度は移動体横軸に沿ってまっすぐとなる.[図2.13(c)]
Figure:
2自由度の移動(a)(b)(c)
![\begin{figure}
\begin{center}
\psbox [width=10.08cm]{F33.eps}
\end{center}
\end{figure}](img77.gif) |
Figure:
4車輪の移動装置の設計
![\begin{figure}
\begin{center}
\psbox [width=15.11cm]{F34.eps}
\end{center}
\end{figure}](img78.gif) |
Figure:
基本移動操作(a)(b)(c)
![\begin{figure}
\begin{center}
\psbox [width=9.80cm]{F35.eps}
\end{center}
\end{figure}](img79.gif) |



Next: 一般的な4輪移動体の運動学
Up: ある方向にスライドする車輪の場合
Previous: 運動の制御能力
Contents
Shoichiro FUJISAWA
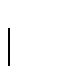 となる.[図2.13(a)].以下の式のように,任意の原点で,位置座標
となる.[図2.13(a)].以下の式のように,任意の原点で,位置座標 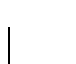 [図2.13(b)と等しくなければならない.以下の式のように,任意の原点で位置座標は車輪回転数と関係がある.
[図2.13(b)と等しくなければならない.以下の式のように,任意の原点で位置座標は車輪回転数と関係がある.